Question

A vehicle is at rest on a banked road with angle of banking \[\theta \]. The normal reaction of the vehicle is ${N_1}$. When the vehicle takes a turn on the same road the normal reaction is ${N_2}$. Then $\dfrac{{{N_1}}}{{{N_2}}}$ is equal to
A. $1$
B. ${\sin ^2}\theta $
C. ${\cos ^2}\theta $
D. $0.5\sin (2\theta )$

Answer 1

Hint: A phenomenon in which the edges of roads are raised to curve above the inner edge in order to provide the required centripetal force so that the vehicles can take a turn is known as banking of roads. The angle at which the vehicle is inclined with the road is called angle of banking.

Complete answer:
Step I:
The normal force on the vehicle when it takes a turn around the curved road is given by
$ \Rightarrow $$N = mg$

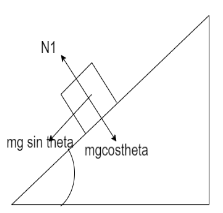
Before taking the turn, the normal force on the vehicle is given as
$ \Rightarrow $${N_1} = mg\cos \theta $ -----------(i)
Step II:
But when the vehicle takes a turn, then centripetal force will act on the vehicle. The normal force then acting on the vehicle is given by
$ \Rightarrow $${N_2} = mg\cos \theta + \dfrac{{m{v^2}}}{r}\sin \theta $ ---------(ii)
Step III:
While turning around the road, the vehicle makes an angle of banking with the road. The angle of banking is given by the relation:
$ \Rightarrow $$\tan \theta = \dfrac{{{v^{^2}}}}{{rg}}$
$ \Rightarrow $$\dfrac{{{v^2}}}{r} = g\tan \theta $ --------(iii)
Step IV:
Substitute the value from equation (iii) in equation (ii)
$ \Rightarrow $${N_2} = mg\cos \theta + mg\tan \theta \sin \theta $
Step V:
Taking their ratios
$ \Rightarrow $\[\dfrac{{{N_1}}}{{{N_2}}} = \dfrac{{mg\cos \theta }}{{mg\cos \theta + mg\tan \theta \sin \theta }}\]
$\Rightarrow \dfrac{{{N_1}}}{{{N_2}}}= \dfrac{{mg\cos \theta }}{{mg\cos \theta + mg\dfrac{{\sin \theta }}{{\cos \theta }}\sin \theta }}$
$\Rightarrow \dfrac{{{N_1}}}{{{N_2}}} = \dfrac{{mg\cos \theta }}{{\dfrac{{mg{{\cos }^2}\theta + mg{{\sin }^2}\theta }}{{\cos \theta }}}}$
$\Rightarrow \dfrac{{{N_1}}}{{{N_2}}} = \dfrac{{mg{{\cos }^2}\theta }}{{mg({{\cos }^2}\theta + {{\sin }^2}\theta )}}$
$\Rightarrow \dfrac{{{N_1}}}{{{N_2}}} = \dfrac{{mg{{\cos }^2}\theta }}{{mg}}$
$\Rightarrow \dfrac{{{N_1}}}{{{N_2}}}= {\cos ^2}\theta $

The ratio will be ${\cos ^2}\theta $. Hence Option C is the right answer.

Note:
It is to be noted that banking of roads is necessary because the horizontal component of the normal force provides necessary centripetal force to the vehicle. If the roads are not banked the vehicles can slip because of the less centripetal force.