Question

A vector $\vec {A}$ is rotated by a small angle $\Delta \theta$ radians ($\Delta \theta << 1$) to get a new vector $\vec {B}$. In that case $|\vec{A}-\vec {B}|$ is
A. $|\vec{A}| (1-\dfrac {\Delta {\theta}^{2}}{2})$
B. 0
C. $|\vec{A}| \Delta \theta$
D. $|\vec{B}| \Delta \theta - |\vec{A}|$

Answer 1

Hint: It is mentioned that the angle between the two vectors is very small. So, the rotation can be neglected and we can consider one vector to be equal to another. Now, use the formula for resultant magnitude of two vectors. Substitute the values in the formula. Then, substitute $|\vec{A}|= |\vec{B}|$ and solve the equation. Thus, find the value of the resultant magnitude of two vectors i.e. $|\vec{A}-\vec {B}|$.

Complete step by step answer:

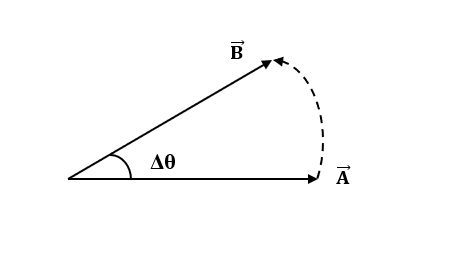
It is given that the change in vector is very small ($\Delta \theta <<1$).
$\therefore|\vec{A}|= |\vec{B}|$ …(1)
The resultant magnitude of two vectors is given by,
$|\vec{A}-\vec {B} |=\sqrt { { |\overrightarrow { A } | }^{ 2 }+{ |\overrightarrow { B } | }^{ 2 }-2|\overrightarrow { A } ||\overrightarrow { B } |\cos {\Delta \theta } }$
Substituting equation. (1) in above equation we get,
$|\vec {A}- \vec {B}|=\sqrt { { |\overrightarrow { A } | }^{ 2 }+{ |\overrightarrow { A } | }^{ 2 }-2|\overrightarrow {{ A}^{2} } |\cos {\Delta \theta } }$
$\Rightarrow |\vec {A}- \vec {B} |= \sqrt {2{|\vec A|}^{2}- 2|\overrightarrow {{ A}^{2} } |\cos {\Delta \theta } }$
$\Rightarrow |\vec {A}- \vec {B}|= 2 |\vec {A}| \sqrt{\dfrac {(1-\cos {\Delta \theta})}{2}}$
$\Rightarrow |\vec{A}-\vec {B} |= 2 |\vec {A}| \sqrt {{\sin}^{2}({\dfrac {\Delta \theta}{2}})}$
$\Rightarrow |\vec{A}-\vec {B}|= 2 |\vec {A}| \sin {\dfrac {\Delta \theta}{2}}$ …(2)
As $\Delta \theta <<1$,
$\dfrac {\Delta \theta }{2}<<1$.
$\therefore \sin {\dfrac {\Delta \theta}{2}} \approx \dfrac {\Delta \theta}{2}$ …(3)
Substituting equation. (2) in equation. (3) we get,
$|\vec{A}-\vec {B} |= 2| \vec {A}| \times \dfrac {\Delta \theta}{2}$
$| \vec{A}-\vec {B}|= |\vec {A}| \Delta \theta$

So, the correct answer is “Option C”.

Note: Students must remember that while adding two vectors don’t only consider the magnitude of the vectors but also consider the direction of both the vectors. If you don’t consider the direction then there might be an error in your calculation. Students must understand that if we double the resultant vector and reverse one of the vectors then the resultant vector gets doubled again.