Question

A vector $\overrightarrow{r}$ is equally inclined with the coordinate axis. If the tip of $\overrightarrow{r}$ is in the first octant and $\left| \overrightarrow{r} \right|=\sqrt{3}$, then $\overrightarrow{r}$ is
$\begin{align}
  & \text{A}\text{. }2\sqrt{3}\left( \widehat{i}-\widehat{j}+\widehat{k} \right) \\
 & \text{B}\text{. }2\sqrt{3}\left( -\widehat{i}+\widehat{j}+\widehat{k} \right) \\
 & \text{C}\text{. }2\sqrt{3}\left( \widehat{i}+\widehat{j}-\widehat{k} \right) \\
 & \text{D}\text{. }\left( \widehat{i}+\widehat{j}+\widehat{k} \right) \\
\end{align}$

Answer 1

- Hint: To calculate the expression for a given vector, we will assume the coefficients of each unit vector associated with the given vector, and will calculate the magnitude of the vector using the same expression. On comparing the magnitude of vector obtained from the assumed coefficients with the given magnitude of the vector, we can obtain the exact expression for the given vector.

Complete step-by-step solution
Vector is described as a quantity that has both magnitude and direction. A vector is typically represented by an arrow whose direction is the same as that of the quantity and whose length is proportional to the magnitude of the quantity. Although a vector has both magnitude and direction, it does not have position. It can be located anywhere in the space.
If a vector is equally inclined to coordinate axis, it means that the vector makes an equal angle with all the three axes; x-axis, y-axis, and z-axis.

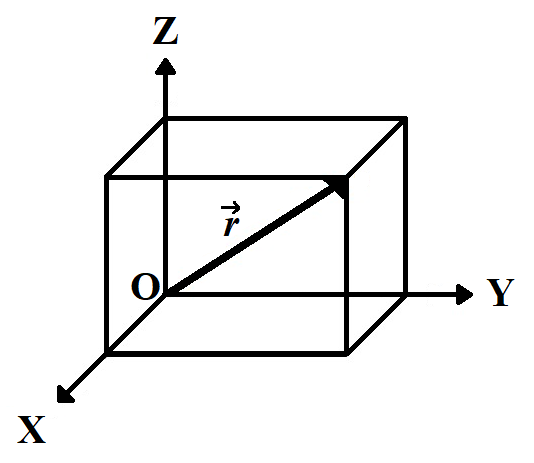
Let’s assume vector $\overrightarrow{r}$ as,
$\overrightarrow{r}=\lambda \widehat{i}+\beta \widehat{j}+\gamma \widehat{k}$
Taking dot product of vector $\overrightarrow{r}$ with unit vectors $\widehat{i},\text{ }\widehat{j},\text{ and }\widehat{k}$
$\overrightarrow{r}\cdot \widehat{i}=\overrightarrow{r}\cdot \widehat{j}=\overrightarrow{r}\cdot \widehat{k}$
The dot product of two vectors is expressed as the product of the magnitude of the two vectors and the cosine of the angle between them. As the vectors $\widehat{i},\text{ }\widehat{j},\text{ and }\widehat{k}$ are the unit vectors associated with the coordinate axis; x-axis, y-axis, and z-axis respectively; it means that all the three unit vectors have magnitude unity, and vector $\overrightarrow{r}$is equally inclined to the three coordinate axis. Therefore, the dot product of vector $\overrightarrow{r}$ with any of the unit vector will generate the same result
It means that,
$\lambda =\beta =\gamma $
(Let’s say equation 1)
Also, it is given that the magnitude of vector $\overrightarrow{r}$ is $\sqrt{3}$
$\left| \overrightarrow{r} \right|=\sqrt{3}$
That is,
$\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}+{{\gamma }^{2}}}=\sqrt{3}$
(Let’s say equation 2)
From equation 1 and equation 2,
$\alpha =\beta =\gamma =1$
Therefore, vector $\overrightarrow{r}$ is given as,
$\overrightarrow{r}=\widehat{i}+\widehat{j}+\widehat{k}$
Hence, the correct option is D.

Note: It should be noted that if a vector is lying in space and equally inclined to the three coordinate axes; it implies that the vector makes an equal angle with each of the coordinate axes. If we take a dot product of that vector with any of the axes, we will get the same quantity. The dot product of two vectors is expressed as the product of the magnitude of the two vectors and the cosine of the angle between them.