Question

A vector \[\overrightarrow{P}\] makes an angle of \[10{}^\circ \] and \[\overrightarrow{Q}\] makes an angle of \[100{}^\circ \]with x-axis. The magnitude of these vectors is 6 m and 8 m. The resultant of these vectors is:
A. 10 m
B. 14 m
C. 2 m
D. none of these

Answer 1

Hint: In this question we have been given two vectors at an angle with the X-axis. We have been asked to calculate the resultant vector of the two given vectors. We have been asked to calculate the magnitude of the vector since in the given options only magnitude of resultant is provided. We shall calculate the resultant vector using the formula for vector addition of two vectors having a specific angle say \[\theta \] between them.

Complete step-by-step solution
It is given that vector P makes an angle of 10 degrees with the X-axis and Q makes an angle 100 degrees with the x-axis as shown in the figure below.

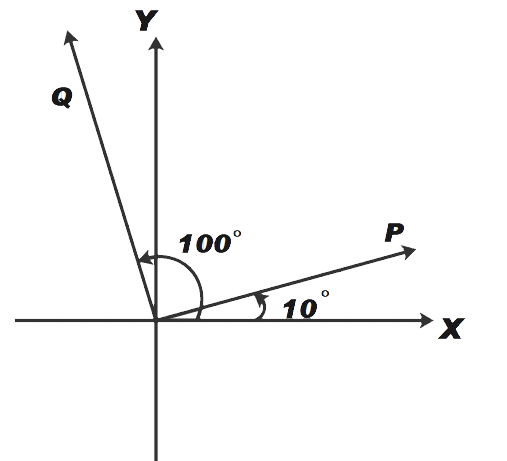
Now, we know that angle between the vectors,
\[\theta =100{}^\circ -10{}^\circ =90{}^\circ \]
Now, we have been asked to calculate the magnitude of the vector.
We know that, the magnitude of resultant vector, say ‘R’ of two vectors having angle \[\theta \] between them is given by,
\[R=\sqrt{{{P}^{2}}+{{Q}^{2}}+2PQ\cos \theta }\]
After substituting the values,
We get,
\[R=\sqrt{{{6}^{2}}+{{8}^{2}}+2\times 6\times 8\cos 90{}^\circ }\]
On solving,
We get,
\[R=10m\]
Therefore, the correct answer is option A.

Note: A vector is a quantity or object having a certain magnitude and direction. The physical quantities such as force, momentum, displacement, etc are said to be vector quantities as they have a direction as well as magnitude. The resultant vector is the addition of two or more vectors. The addition of vectors can be done by many rules such as the parallelogram rule for vector addition.