Question

A vector of length $l$ is turned through the angle $\theta $ about its tail. What is the change in the position vector of its head?

Answer 1

Hint: Here, we have two positions of the same vector. One is its initial position and the other is, when it is turned through an angle $\theta $, about its tail. So, there will be a change in its head position. We need to find this change between initial and final position of head. We can use triangle law to determine this change.
Formula used:
\[\] $\Delta r=\sqrt{\left( {{A}^{2}}+{{B}^{2}}-2AB\cos \theta \right)}$

Complete answer:

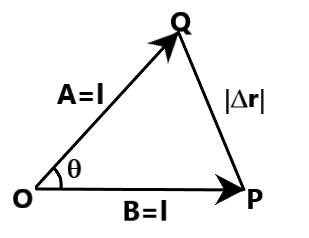
From the figure given above, we can understand that $\overrightarrow{OP}$ is the initial position vector of the head, with $P$ being the head of the vector and $O$, its tail. Then, this vector is rotated over an angle $\theta $, about its tail. Now, the position vector of head is represented as $\overrightarrow{OQ}$, with $Q$ being the head and $O$, its tail. Clearly, these two vectors form the two arms of a triangle $OQP$, as shown.
Now, we can use the triangular law of subtraction to find the change in position of head. Using this law, if two vectors are formed as two sides of a triangle, their difference is given by the third side, taken in the opposite direction. Hence, if $\Delta r$ represents the magnitude of difference in position vectors of head, then, $\Delta r$ is given by
$\Delta r=\sqrt{\left( {{A}^{2}}+{{B}^{2}}-2AB\cos \theta \right)}$
where
$\Delta r$ is the magnitude of difference in initial position vector and final position vector of head
$A$ and $B$are the magnitudes of initial and final position vectors of head
$\theta $ is the angle between initial position vector and final position vector of head
Let this be equation 1.
From the question, magnitudes of both vectors are given to be $l$. Therefore, using equation 1, we have
$\begin{align}
  & \Rightarrow \Delta r=\sqrt{\left( {{l}^{2}}+{{l}^{2}}-2{{l}^{2}}\cos \theta \right)} \\
 & \Rightarrow \Delta r=\sqrt{\left( 2{{l}^{2}}-2{{l}^{2}}\cos \theta \right)} \\
 & \Rightarrow \Delta r=\sqrt{2{{l}^{2}}\times \left( 1-\cos \theta \right)} \\
 & \Rightarrow \Delta r=\sqrt{2{{l}^{2}}\left( 2{{\sin }^{2}}\dfrac{\theta }{2} \right)} \\
\end{align}$
Since, $1-\cos \theta =2{{\sin }^{2}}\dfrac{\theta }{2}$
$\begin{align}
  &\Rightarrow \Delta r=\sqrt{\left( 4{{l}^{2}}{{\sin }^{2}}\dfrac{\theta }{2} \right)} \\
 & \Rightarrow \Delta r=2l\sin \dfrac{\theta }{2} \\
\end{align}$
Therefore, the change in position is equal to $2l\sin \dfrac{\theta }{2}$.

Note:
There might be a tendency to use parallelogram law instead of triangular law. But we need to note that what is required is the change in position (distance), and not a resultant vector. The magnitude of resultant vector using parallelogram law is given by
$\Delta r=\sqrt{\left( {{A}^{2}}+{{B}^{2}}+2AB\cos \theta \right)}$