Question

A variable plane is at a constant distance p from the origin and meets the axes in A, B and C. The locus of the centroid of the triangle ABC is
(a) \[{{x}^{-2}}+{{y}^{-2}}+{{z}^{-2}}={{p}^{-2}}\]
(b) \[{{x}^{-2}}+{{y}^{-2}}+{{z}^{-2}}=4{{p}^{-2}}\]
(c) \[{{x}^{-2}}+{{y}^{-2}}+{{z}^{-2}}=16{{p}^{-2}}\]
(d) \[{{x}^{-2}}+{{y}^{-2}}+{{z}^{-2}}=9{{p}^{-2}}\]

Answer 1

Hint: We can assume the coordinates of the points A, B and C as $\left( a,0,0 \right)$, $\left( 0,b,0 \right)$ and $\left( 0,0,c \right)$. From these coordinates, we can determine the coordinates of the centroid of the triangle ABC as $x=\dfrac{a}{3},y=\dfrac{b}{3},z=\dfrac{c}{3}$. Also, the equation of the plane, from the intercept form can be determine as $\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1$. From this equation, we can determine the distance of the plane from the origin, which is given to be equal to p, in terms of a, b and c. The values of a, b and c can be substituted in terms of the coordinates of the centroid given as $x=\dfrac{a}{3},y=\dfrac{b}{3},z=\dfrac{c}{3}$ to get the final equation of the locus of the centroid.

Complete step by step solution:
Let the coordinates of the points A, B and C be $\left( a,0,0 \right)$, $\left( 0,b,0 \right)$ and $\left( 0,0,c \right)$, so that the plane will look like

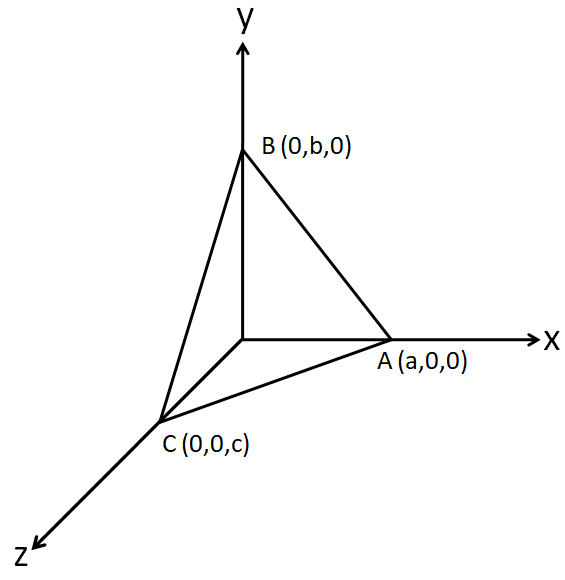
Therefore, the x coordinate of the triangle ABC becomes
$\begin{align}
  & \Rightarrow x=\dfrac{a+0+0}{3} \\
 & \Rightarrow x=\dfrac{a}{3}......\left( i \right) \\
\end{align}$
Similarly, the y and the z coordinates can be given by
$\begin{align}
  & \Rightarrow y=\dfrac{b}{3}......\left( ii \right) \\
 & \Rightarrow z=\dfrac{c}{3}......\left( iii \right) \\
\end{align}$
Multiplying the equation (i) by $3$ we get
$\Rightarrow a=3x......\left( iv \right)$
Similarly, from the equations (ii) and (iii) we obtain
$\begin{align}
  & \Rightarrow b=3y.......\left( v \right) \\
 & \Rightarrow c=3z.......\left( vi \right) \\
\end{align}$
From the intercept form of the equation of a plane, we can write the equation of the given plane as
$\begin{align}
  & \Rightarrow \dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1 \\
 & \Rightarrow \dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}-1=0 \\
\end{align}$
According to the question, the distance of the plane from the origin is equal to p. Thereofr, we can write
$\begin{align}
  & \Rightarrow p=\dfrac{\left| \dfrac{0}{a}+\dfrac{0}{b}+\dfrac{0}{c}-1 \right|}{\sqrt{{{\left( \dfrac{1}{a} \right)}^{2}}+{{\left( \dfrac{1}{b} \right)}^{2}}+{{\left( \dfrac{1}{c} \right)}^{2}}}} \\
 & \Rightarrow p=\dfrac{1}{\sqrt{{{\left( \dfrac{1}{a} \right)}^{2}}+{{\left( \dfrac{1}{b} \right)}^{2}}+{{\left( \dfrac{1}{c} \right)}^{2}}}} \\
\end{align}$
Taking the reciprocals of both the sides, we get
$\Rightarrow \dfrac{1}{p}=\sqrt{{{\left( \dfrac{1}{a} \right)}^{2}}+{{\left( \dfrac{1}{b} \right)}^{2}}+{{\left( \dfrac{1}{c} \right)}^{2}}}$
Now, taking the squares of both the sides, we get
$\begin{align}
  & \Rightarrow {{\left( \dfrac{1}{p} \right)}^{2}}={{\left( \dfrac{1}{a} \right)}^{2}}+{{\left( \dfrac{1}{b} \right)}^{2}}+{{\left( \dfrac{1}{c} \right)}^{2}} \\
 & \Rightarrow \dfrac{1}{{{p}^{2}}}=\dfrac{1}{{{a}^{2}}}+\dfrac{1}{{{b}^{2}}}+\dfrac{1}{{{c}^{2}}} \\
\end{align}$
Substituting the equations (iv), (v) and (vi) we get
\[\begin{align}
  & \Rightarrow \dfrac{1}{{{p}^{2}}}=\dfrac{1}{{{\left( 3x \right)}^{2}}}+\dfrac{1}{{{\left( 3y \right)}^{2}}}+\dfrac{1}{{{\left( 3z \right)}^{2}}} \\
 & \Rightarrow \dfrac{1}{{{p}^{2}}}=\dfrac{1}{9{{x}^{2}}}+\dfrac{1}{9{{y}^{2}}}+\dfrac{1}{9{{z}^{2}}} \\
\end{align}\]
Multiplying both sides by \[9\] we get
$\begin{align}
  & \Rightarrow \dfrac{9}{{{p}^{2}}}=\dfrac{1}{{{x}^{2}}}+\dfrac{1}{{{y}^{2}}}+\dfrac{1}{{{z}^{2}}} \\
 & \Rightarrow 9{{p}^{-2}}={{x}^{-2}}+{{y}^{-2}}+{{z}^{-2}} \\
 & \Rightarrow {{x}^{-2}}+{{y}^{-2}}+{{z}^{-2}}=9{{p}^{-2}} \\
\end{align}$
Thus, the locus of the triangle ABC is found out to be ${{x}^{-2}}+{{y}^{-2}}+{{z}^{-2}}=9{{p}^{-2}}$.

So, the correct answer is “Option d”.

Note: For solving these kinds of questions, we need to remember the different forms of the equation of a plane. Also, we need to remember the coordinates of the centroid of a triangle, which are equal to the average of the coordinates of its vertices. Do not forget the square root sign in the distance formula.