Question

A variable force F=at is applied on a block of mass m from time t=0, kept on a smooth horizontal surface. Find the velocity of the block at the instant it leaves the surface.

Answer 1

Hint: For any body in a motion, the equations of equilibrium are
$
\sum\limits_{}^{} {{F_x} = m{a_x}} \\
\implies \sum\limits_{}^{} {{F_y} = m{a_y}} \\
\implies \sum\limits_{}^{} {{M_z} = 0} \\
$
We have to first draw the free body diagram of the body then we have to balance forces in both X and Y axis. As force here is a variable force, we have to calculate the velocity in a small interval and then we have to integrate with respect to time (dt).
This formula of integration will be used, $\int {{x^n}dx} = \dfrac{{{x^{n + 1}}}}{{n + 1}}$

Complete step by step answer:
Let us first see the free body diagram of the body:
 

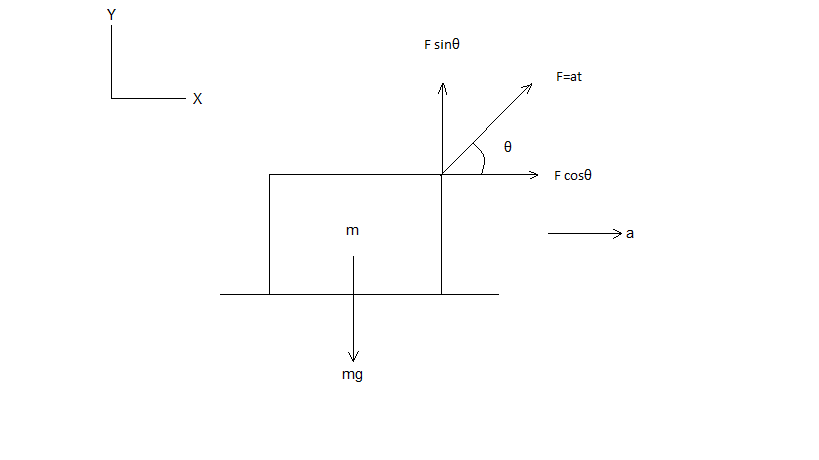
From the free body diagram it is clear that for the application of force F there will be a motion in the positive X axis with acceleration a (let) in the direction of the positive X axis. There is no acceleration in Y direction.
As, force is inclined with angle $\theta $with respect to horizontal, the components of F are drawn.
At, t=0, velocity of the body, v= 0 and the velocity of the block at the instant when it leaves the surface is V.
Now, $\sum\limits_{}^{} {{F_y} = m{a_y}} $
Then,
$F\sin \theta - mg = 0$
$\implies at\sin \theta = mg[\because F = at]$
$\implies t = \dfrac{{mg}}{{a\sin \theta }}$………………………………………………..(1)
Also,
$\sum\limits_{}^{} {{F_x} = m{a_x}} $
$\implies F\cos \theta = ma$
$\implies at\cos \theta = m\dfrac{{dv}}{{dt}}[\because F = at,a = \dfrac{{dv}}{{dt}}]$
$\implies at\cos \theta dt = mdv$
Integrating both sides, $\int\limits_0^t {at\cos \theta dt} = \int\limits_0^V {mdv} $
$a\cos \theta \int\limits_0^t {tdt} = m\int\limits_0^V {dv} $
$\implies a\cos \theta [\dfrac{{{t^2}}}{2}]_0^t = m[v]_0^V$
$\implies mV = a\cos \theta \dfrac{{{t^2}}}{2}$
$\implies mV = a\cos \theta \dfrac{{{{(\dfrac{{mg}}{{a\sin \theta }})}^2}}}{2}[from(1)]$
$\therefore V = \dfrac{{a\cos \theta }}{m} \times \dfrac{{{m^2}{g^2}}}{{2{a^2}{{\sin }^2}\theta }} = \dfrac{{m{g^2}\cos \theta }}{{2a{{\sin }^2}\theta }}$

So, the velocity of the block at the instant it leaves the surface =$\dfrac{{m{g^2}\cos \theta }}{{2a{{\sin }^2}\theta }}$.

Note:
If there is an initial velocity, v at time, t=0 then we have to integrate velocity from v to V like $a\cos \theta \int\limits_0^t {tdt} = m\int\limits_v^V {dv} $.