Question

A U-tube of uniform cross section is partially filled with a liquid 1. Another liquid 2 which will not mix with the liquid 1 is poured into one side. It is found that the liquid levels of the two sides of the tube are the same, while the level of liquid 1 has risen by $2cm$ . If the specific gravity of liquid I is $1.1$, the specific gravity of liquid 2 will be:

$\begin{align}
  & A.1.12 \\
 & B.1.1 \\
 & C.1.05 \\
 & D.1.0 \\
\end{align}$

Answer 1

Hint: From the figure and the conditions mentioned in the question, we can see that the height of the liquid column 1 in the right limb will be $\left( h+2 \right)cm$. The height of the liquid column 2 in the left limb is $2cm$ and of liquid column 1 is $hcm$. Substitute these details and compare them in the equation of,
$h\rho g=\text{constant}$
These details will help you to solve this problem.

Complete answer:
First of all let us analyse the figure in the question.

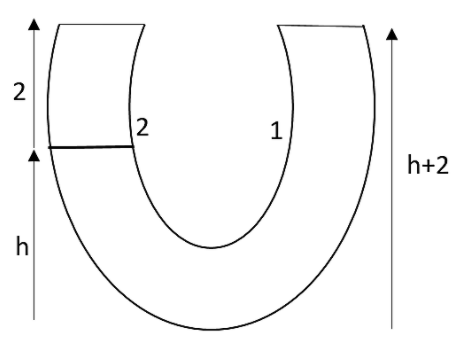
From this figure, we can say that the height of the liquid column 1in the left limb is $hcm$. The height of the liquid column 2 in the left thumb will be $hcm$. And in the case of the right limb, it will be $\left( h+2 \right)cm$.
Specific gravity of liquid column 1 is written as,
${{\rho }_{1}}=1.1$
Therefore we can write that,
$2\times {{\rho }_{2}}\times g+h\times 1.1\times g=\left( 2+h \right)\times 1.1\times g$
From this equality relationship, we can cancel the common terms on the both sides, so that we can write that,
$2\times {{\rho }_{2}}+h\times 1.1=\left( 2+h \right)\times 1.1$
Expanding the bracket will be given as,
$2\times {{\rho }_{2}}+h\times 1.1=\left( 2.2+h\times 1.1 \right)$
From this the specific gravity of the liquid 2 can be found by rearranging the terms,
$\begin{align}
  & 2{{\rho }_{2}}=2.2 \\
 & \Rightarrow {{\rho }_{2}}=1.1 \\
\end{align}$
Therefore the specific gravity of the liquid 2 has been obtained.

Hence the correct answer is option B.

Note:
The specific gravity is defined as the ratio between the densities of a body with respect to a reference substance. The specific gravity can be useful in saying whether an object will float or sink in the reference substance based on its value. It is also known as the relative density.