Question

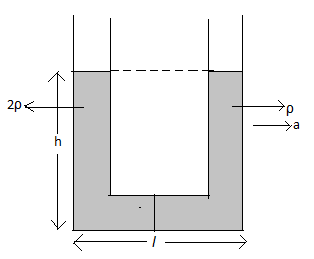
A U-tube of base length ‘\[l\]’ is filled with the same volume of two liquids of densities \[\rho \] and \[2\rho \] is moving with an acceleration ‘\[a\]’ on the horizontal plane. If the height difference between the two surfaces (open to atmosphere) becomes zero then the height \[h\] is given by

A. \[\dfrac{a}{{2g}}l\]
B. \[\dfrac{{3a}}{{2g}}l\]
C. \[\dfrac{a}{g}l\]
D. \[\dfrac{{2a}}{{3g}}l\]

Answer 1

Hint: Use the formula of pressure-depth relation. This formula gives the relation between the atmospheric pressure, density of liquid, acceleration of liquid and depth.

Formula used:
The pressure \[P\] at a depth \[h\] is given by
\[P = {P_0} + \rho gh\] …… (1)
Here, \[{P_0}\] is the atmospheric pressure, \[\rho \] is the density and \[g\] is the acceleration due to gravity.

Complete step by step answer:
A U-tube of base length ‘\[l\]’ is filled with the same volume of two liquids of densities \[\rho \] and \[2\rho \] which are moving with an acceleration ‘\[a\]’ on the horizontal plane.
Redraw the diagram of the U-tube.

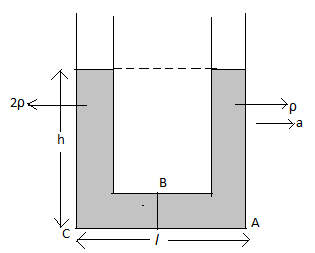
The liquid with the density \[2\rho \] must be moving slowly as compared to the liquid with the density \[\rho \].
The liquids have the acceleration \[a\] only in the horizontal plane and not in the vertical plane.
Using equation (1), determine the pressure \[{P_A}\] at point A considering the right column of the U-tube.
\[{P_A} = {P_0} + \rho gh\]
Using equation (1), determine the pressure \[{P_B}\] at point B from point A considering the right column of the U-tube.
\[{P_B} = {P_A} + \rho a\dfrac{l}{2}\]
Substitute \[{P_0} + \rho gh\] for \[{P_A}\] in the above equation.
\[{P_B} = {P_0} + \rho gh + \rho a\dfrac{l}{2}\]
Using equation (1), determine the pressure \[{P_C}\] at point C from point B considering the right column of the U-tube.
\[{P_C} = {P_B} + 2\rho a\dfrac{l}{2}\]
Substitute \[{P_0} + \rho gh + \rho a\dfrac{l}{2}\] for \[{P_B}\] in the above equation.
\[{P_C} = {P_0} + \rho gh + \rho a\dfrac{l}{2} + 2\rho a\dfrac{l}{2}\]
\[{P_C} = {P_0} + \rho gh + \dfrac{3}{2}\rho al\] …… (2)
Using equation (1), determine the pressure \[{P_C}\] at point C considering the left column of the U-tube.
\[{P_C} = {P_0} + 2\rho gh\] …… (3)
The height difference between the two surfaces of two liquids open to the atmosphere becomes zero. Hence, the pressure at point C from both right and left liquid columns are the same.
Equate equation (2) and (3).
\[{P_0} + \rho gh + \dfrac{3}{2}\rho al = {P_0} + 2\rho gh\]
\[ \Rightarrow \dfrac{3}{2}\rho al = \rho gh\]
Rearrange the above equation for height \[h\].
\[h = \dfrac{{\dfrac{3}{2}\rho al}}{{\rho g}}\]
\[ \Rightarrow h = \dfrac{{3a}}{{2g}}l\]
Therefore, the height \[h\] is \[\dfrac{{3a}}{{2g}}l\].

So, the correct answer is “Option B”.


Note:
The pressure-depth relation is not the same for the pressure at the height h.
The height difference between the two surfaces (open to atmosphere) becomes zero.
The average density of a substance or object is defined as its mass per unit volume.