Question

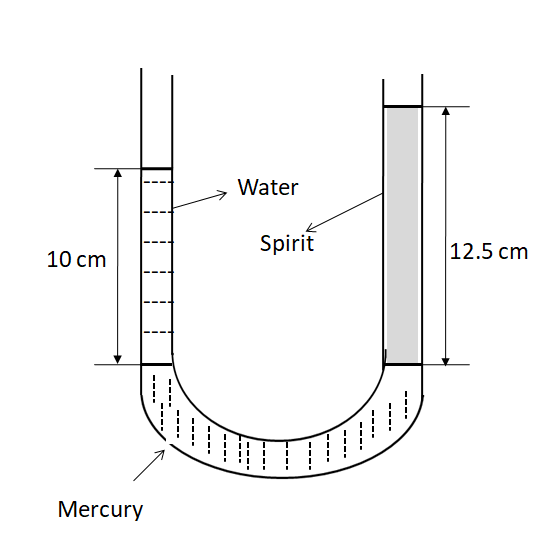
A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two rows are in the same level with $10.0cm$ of water in one arm and $12.5cm$ of spirit in the other. What is the specific gravity of spirit?

Answer 1

Hint: To answer this question, we need to use Pascal's law for the pressure in a fluid. Also, we need to know that the specific gravity of a liquid is its density with respect to the water.

Formula used:
$\Rightarrow P = \rho gh$, where $P$ is the pressure below a liquid column of height $h$ and density $\rho $, and $g$ is the acceleration due to gravity.

Complete step by step solution:
Let ${\rho _w}$ and ${\rho _s}$ be the respective densities of the water and the spirit.
Also, let ${h_1}$ and ${h_2}$ be the heights of the water and the spirit columns respectively.
We know from Pascal's law that inside a fluid, the pressure at the points which are at the same level is constant.
According to the question, the points A and B inside the U-tube in the below figure are at the same level. So the pressures at the points A and B are the same.

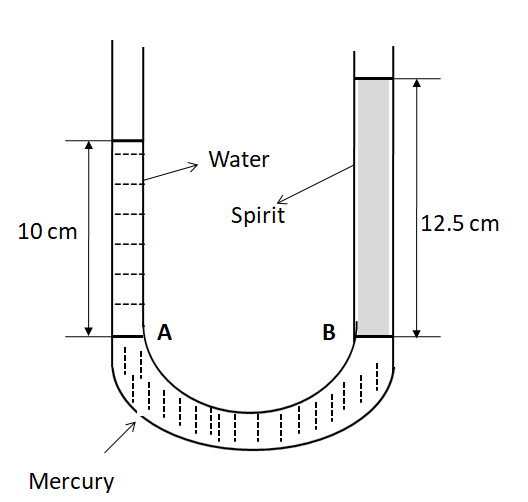
The pressure at the point A
$\Rightarrow {P_A} = {P_o} + {\rho _w}g{h_1}$ …………………..(i)
And the pressure at the point B
$\Rightarrow {P_B} = {P_o} + {\rho _s}g{h_2}$ ……………………….(ii)
(Here ${P_0}$ is the atmospheric pressure)
By Pascal’s law
$\Rightarrow {P_A} = {P_B}$
From (i) and (ii), we have
$\Rightarrow {P_o} + {\rho _w}g{h_1} = {P_o} + {\rho _s}g{h_2}$
Cancelling ${P_0}$ from both the sides, we get
$\Rightarrow {\rho _w}g{h_1} = {\rho _s}g{h_2}$
Dividing by $g$ on both the sides
$\Rightarrow {\rho _w}{h_1} = {\rho _s}{h_2}$
$\Rightarrow \dfrac{{{\rho _s}}}{{{\rho _w}}} = \dfrac{{{h_1}}}{{{h_2}}}$
According to the question, ${h_1} = 10cm$ and ${h_2} = 12.5cm$
$\therefore \dfrac{{{\rho _s}}}{{{\rho _w}}} = \dfrac{{10}}{{12.5}}$
On solving, we get
$\Rightarrow \dfrac{{{\rho _s}}}{{{\rho _w}}} = 0.8$ ……………………..(iii)
As we know that the specific gravity of a liquid is the ratio of its density to the density of water. So, the specific gravity of the spirit
$\Rightarrow S = \dfrac{{{\rho _s}}}{{{\rho _w}}}$
From (iii)
$\Rightarrow S = 0.8$
Hence the specific gravity of the spirit is equal to $0.8$.

Note:
While making the pressure balance using Pascal's law, we don’t need to convert all the quantities in the SI units. We just need to make sure that the respective quantities appearing in the equation must have the same units on both the sides.