Question

A uniform U-tube of length l as shown in the figure is mounted on a horizontal table and accelerated towards right with constant acceleration a. The difference in height of liquids in both the limbs will be

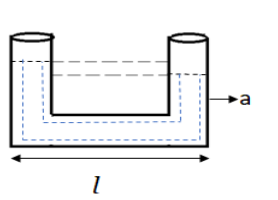
Answer 1

Hint: The height difference between liquids in both the limbs is calculated by applying the principle of Bernoulli’s equation. Bernoulli's equation is applied on either side of the limbs. Then, the principle of equating the pressure in both the right limb and left limb are applied. By equating the pressure, we will get the difference in height of liquids between both the limbs.
Formula used:
\[{{P}_{0}}+\text{ }\rho gh\text{ }=\text{ }{{P}_{0}}+\dfrac{F}{A}\]
Where,
\[\rho \] is the density of the fluid
g is the acceleration due to gravity
h is the height of rise of water or the difference in height in both the limbs
\[{{P}_{0}}\] is the pressure of the fluid in the U-tube manometer
F is the force
A is the area of the U-tube manometer

Complete answer:
Generally,
We know that in a U-tube manometer,
Pressure in the left limb is equal to the pressure in the right limb
Let us consider a point B in a U-tube manometer.
Let h be the height difference between both the limbs.

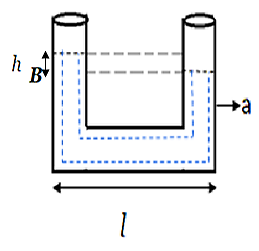
At point B,
Input the formula
\[{{P}_{0}}+\text{ }\rho gh\text{ }=\text{ }{{P}_{0}}+\dfrac{F}{A}\] ----- (1)
Let the above formula be equation (1)
Substitute the value of force as in equation (1),
\[F\text{ }=\text{ }ma\]
Where, m is the mass, a is the acceleration.
We get
\[\rho gh\text{ }=\dfrac{ma}{A}\]----- (2)
This becomes equation (2)
Now, substitute the value of mass as
\[m\text{ }=\text{ }\rho V\]in equation (2)
Where,
V is the volume of water
The equation becomes
\[\rho gh\text{ }=\dfrac{\rho Va}{A}\]----- (3)
This becomes equation (3)
Then, substitute the value of volume as
\[V\text{ }=\text{ }Ar\]in equation (3)
Where, r is the radius.
We get the equation as,
\[\rho gh\text{ }=\dfrac{\rho Ara}{A}\]----- (4)
This becomes equation (4)
In this equation, density and area get cancelled and the equation becomes,
\[gh\text{ }=\text{ }ra\]----- (5)
Let it be equation (5)
From the above equation, we finally get the difference in height in both the limbs as
\[h\text{ }=~\dfrac{ar}{g}\]----- (6)
Consider it as equation (6)
Therefore, the answer is
\[h\text{ }=~\dfrac{ar}{g}\]

Note:
If different fluids are present, the values of density of fluid varies. Also, pressure exerted in both the limbs varies. In such cases, the pressure difference is given by the formula,
\[P={{P}_{1}}-{{P}_{2}}\]
Where,
\[{{P}_{1}}\] and \[{{P}_{2}}\] are pressures in both the limbs. From the above formula, the height difference is obtained.