Question

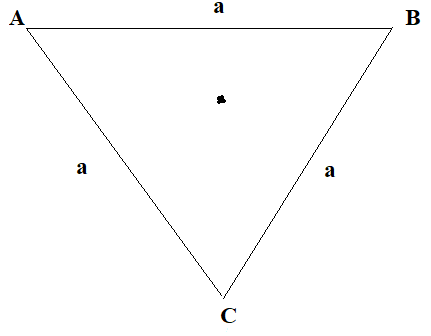
A uniform triangular plate \[ABC\] of moment of mass \[m\] and inertia \[I\] (about an axis passing through A and perpendicular to plane of the plate) can rotate freely in the vertical plane about point ′ \[A\] ′ as shown in figure. The plate is released from the position shown in the figure. Line \[AB\] is horizontal. The acceleration of centre of mass just after the release of plate is:

A. \[\dfrac{{mg{a^2}}}{{\sqrt 3 I}}\]
B. \[\dfrac{{mg{a^2}}}{{4I}}\]
C. \[\dfrac{{mg{a^2}}}{{2\sqrt 3 I}}\]
D. \[\dfrac{{mg{a^2}}}{{3I}}\]

Answer 1

Hint: First of all, we will draw the diagram which shows all the length of the sides used for the calculation of torque and the acceleration. All the medians intersect at a point which is in a ratio \[2:1\] . We will manipulate accordingly to obtain the result.

Complete step by step answer:
In the given question, we are supplied the following data:
There is a uniform triangular plate \[ABC\] whose moment of mass is \[m\] and inertia \[I\] .
The triangular plate is rotating about an axis passing through \[A\] and perpendicular to the plane of the plate.
The line labelled as \[AB\] is in horizontal position.
We are asked to find the acceleration of the centre of mass just after the release of plate.

To begin with, we will first observe the situation as given in the question, we know that the triangle is an equilateral one. All the medians will intersect at a common point. In an equilateral triangle, always the medians intersect in a ratio \[2:1\] .
For better understanding, we will draw a diagram, showing the various sides and the weight of the triangular plate, which acts through the centre of mass.

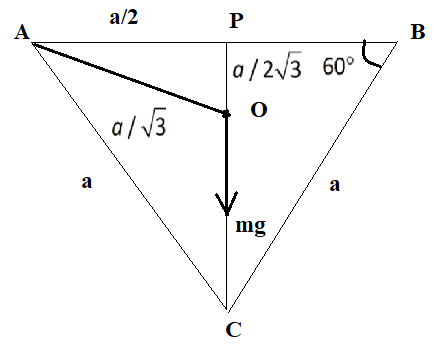
In the diagram, we can see that in the triangle, the median is in a ratio, \[OC:OP = 2:1\] .
All the sides have a length of \[a\] and the vertex has angles \[60^\circ \] .
Let us proceed to solve the problem.
In the triangle \[PCB\] , we apply trigonometric ratio of sine of the angle:
$\sin 60^\circ = \dfrac{{PC}}{{BC}} \\
\Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{PC}}{a} \\
\Rightarrow PC = a \times \dfrac{{\sqrt 3 }}{2} \\$
Since, the median is in a ratio, \[OC:OP = 2:1\] .
We can calculate the length of \[OP\] .
$OP = \dfrac{1}{{1 + 2}} \times a \times \dfrac{{\sqrt 3 }}{2} \\
\Rightarrow OP = \dfrac{1}{3} \times a \times \dfrac{{\sqrt 3 }}{2} \\
\Rightarrow OP = \dfrac{a}{{2\sqrt 3 }} \\$
By using Pythagoras theorem in the \[AOP\] , we now calculate the length of the side \[AO\] .
$A{O^2} = O{P^2} + A{P^2} \\
\Rightarrow A{O^2} = {\left( {\dfrac{a}{{2\sqrt 3 }}} \right)^2} + {\left( {\dfrac{a}{2}} \right)^2} \\
\Rightarrow AO = \sqrt {\dfrac{{{a^2}}}{{12}} + \dfrac{{{a^2}}}{4}} \\
\Rightarrow AO = \dfrac{a}{{\sqrt 3 }} \\$
Now, we can find the expression for torque about \[A\] :
$mg \times \dfrac{a}{2} = I\alpha \\
\Rightarrow \alpha = \dfrac{{mga}}{{2I}} \\$
Again, we can find the acceleration, which is given by the following expression:
${\text{Acceleration}} = \dfrac{a}{{\sqrt 3 }} \times \alpha \\
\Rightarrow {\text{Acceleration}} = \dfrac{a}{{\sqrt 3 }} \times \dfrac{{mga}}{{2I}} \\
\Rightarrow {\text{Acceleration}} = \dfrac{{mg{a^2}}}{{2\sqrt 3 I}} \\$
Hence, the acceleration of the centre of mass just after the release of plate is \[\dfrac{{mg{a^2}}}{{2\sqrt 3 I}}\] .

Note:
While solving this problem, we should know that a median is always divided in the ratio \[2:1\] .
Many students seem to have a confusion regarding the length to be taken while calculating the acceleration.
The length that should be taken is the shortest distance between the point about which the object rotates and the centre of mass.