Question

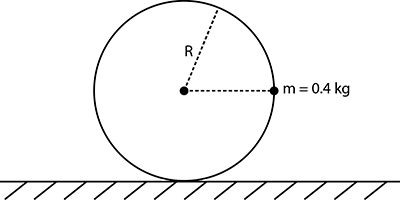
A uniform thin circular ring of mass $m\left( {m = 0.4\,kg} \right)$ and radius has a small particle of the same mass m fixed on it as shown in the figure above. The line joining the particle to centre is initially horizontal. The ground is frictionless. If the contact force (magnitude) exerted by the ground on the ring, when the system is released from rest is $\dfrac{3}{x}mg$, find the value of $x$.

Answer 1

Hint: The angular momentum of a system of particles about a given axis is directly proportional to the external torque applied on the body.

Complete step by step answer:
Since, the mass m is fixed at the horizontal position to the line joining the centre of the ring. So, it will produce a torque. If $I$ be the moment of inertia of the ring and $\alpha $ be the angular acceleration, then from the torque equation we have $mgR = I\alpha $
The moment of inertia of the ring about the centre = $m{R^2}$
As the given point mass lies about the line of tangent to the ring. So, by the theorem of parallel axis, moment of inertia of the ring about the point mass = $m{R^2} + m{R^2}$
$ \Rightarrow mgR = \left( {m{R^2} + m{R^2}} \right)\alpha \Rightarrow \alpha = \dfrac{g}{{2R}}$
The centre of mass of the system lies between the geometric centre of the ring and the point mass.
Writing the force equations, we have $\dfrac{3}{x}mg$
$mg + mg - N = 2m\left( {\dfrac{{R\alpha }}{2}} \right)$
\[\Rightarrow 2mg - N = 2m\left( {\dfrac{{Rg}}{{2 \times 2R}}} \right)
\Rightarrow 2mg - N = \dfrac{{mg}}{2}\]
\[ \Rightarrow N = 2mg - \dfrac{{mg}}{2} \Rightarrow N = \dfrac{{3mg}}{2}\].
So comparing the value of N with $\dfrac{3}{{x}} mg$ we have,
$x = 2.$

Note:
The moment of inertia of a body along the given axis is equal to the torque acting on the body rotating with unit angular acceleration about it. Therefore, $\tau = I\alpha $.
This equation is called the fundamental equation of rotation. This corresponds to $F = m \times a$, which is the fundamental equation of linear motion. Also, a body is in rotational equilibrium if the net external torque or the vector sum of all the torques acting on the body is zero.