Question

A uniform string of length 20m is suspended from a rigid support. A short-wave pulse is introduced at the lowest end. It starts moving up the string. The time taken to reach the support is (Take \[g=10m{{s}^{-2}}\])
A. \[2\pi \sqrt{2}s\]
B. 2s
C. \[2\sqrt{2}s\]
D. \[\sqrt{2}s\]

Answer 1

Hint: The velocity of the pulse formed in a string depends on the Tension and mass distribution. The formula for the velocity of pulse is given below. The tension of a string suspended from support varies with height, In case of string of mass the tension of a point at a distance x form the lower end is given as
\[T=\mu gx\]
Formula used:
\[v=\sqrt{\dfrac{T}{\mu }}\]

Complete answer:
The given string is uniform. That means the mass distribution of the string is constant. Let that be \[\mu \]
\[\mu =\dfrac{m}{L}\]
Where m is the mass of the string and L is the length of the string
We also know that in case of string the velocity of the pulse is given as
\[v=\sqrt{\dfrac{T}{\mu }}\]…..(1)
Where T is the tension on the string.

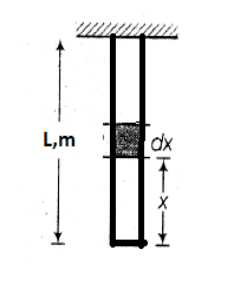
In case of string of mass the tension of a point at a distance x form the lower end is given as
\[T=\mu gx\]
And we also know that \[v=\dfrac{dx}{dt}\]
 So 1 can be written as
\[v=\sqrt{\dfrac{T}{\mu }}\]
\[\begin{align}
  & \Rightarrow \dfrac{dx}{dt}=\sqrt{\dfrac{\mu gx}{\mu }} \\
 & \Rightarrow \dfrac{dx}{dt}=\sqrt{\dfrac{mgx/L}{m/L}} \\
 & \Rightarrow \dfrac{dx}{dt}=\sqrt{g}\sqrt{x} \\
 & \Rightarrow \dfrac{dx}{\sqrt{x}}=\sqrt{g}dt \\
\end{align}\]
Here we have a relation between the distance x from the lower end of the string and time. Integrating both sides of this equation for the entire duration it takes the pulse to reach the top we get
\[\begin{align}
  & \dfrac{dx}{\sqrt{x}}=\sqrt{g}dt \\
 & \Rightarrow \int\limits_{0}^{L}{{{x}^{-1/2}}dx}=\sqrt{g}\int\limits_{0}^{L}{dt} \\
 & \Rightarrow {{\left[ \dfrac{{{x}^{1/2}}}{1/2} \right]}^{L}}_{0}=\sqrt{gt} \\
 & \Rightarrow \dfrac{\sqrt{L}-0}{1/2}=\sqrt{gt} \\
 & \Rightarrow t=\dfrac{2\sqrt{L}}{\sqrt{g}} \\
\end{align}\]
 We now have the time taken by the pulse to reach the support. Plugging in the Values given in question
\[\begin{align}
  & \Rightarrow t=\dfrac{2\sqrt{L}}{\sqrt{g}} \\
 & \Rightarrow t=2\times \sqrt{\dfrac{20}{10}} \\
 & \Rightarrow t=2\sqrt{2}s \\
\end{align}\]
So, the pulse will take \[2\sqrt{2}s\] to reach the support

So, the correct answer is “Option C”.

Note:
Generally, in physics the string taken is considered massless. A massless string has constant tension throughout its length and directed away from connected masses. Meanwhile a string with mass, as in case of the given question, may have varying tension due to its own weight and students should be extra careful when dealing with strings with masses.