Question

A uniform rope of total length l is at rest on a table with fraction f of its length hanging. If the coefficient of friction between the table and the chain is $\mu$ then which of the following relation is true:
$A. f=\mu$
$B. f=\dfrac{1}{1+\mu}$
$C. f=\dfrac{1}{1+\dfrac{1}{\mu}}$
$D. f=\dfrac{\mu}{1+\dfrac{1}{\mu}}$

Answer 1

Hint: We need to find the condition for equilibrium of the system. To do this, we have to calculate the forces on two parts of the rope. Then we have to equal them.

Formula used: $$F(friction)=\mu Mg $$

Complete step-by-step solution:
Let m be the total mass of the rope. The mass of the part that is hanging is fm. And its weight is fmg . Here, g= acceleration due to gravity. And the mass of the remaining part of the rope is (1-f)m. Its weight is (1-f)mg . This is the normal force that is acting on the table and giving rise to the frictional force. Hence frictional force …..

$$F_f=\mu (1-f)mg $$

This has to be equal to the force fmg. This can be clearly understood from the given image.

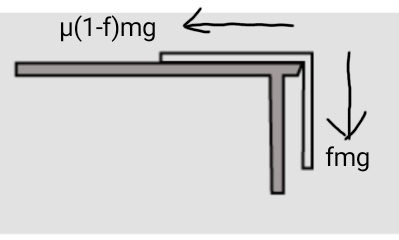
Now equating these two forces …..

$$\mu (1-f)mg=fmg $$
$\Rightarrow\mu (1-f)=f $
$\Rightarrow \mu-\mu f= f$
$\Rightarrow \mu f+f=\mu $
$\Rightarrow f=\dfrac{\mu}{1+\mu}$
$\Rightarrow f=\dfrac{1}{1+\dfrac{1}{\mu}} $

Hence we can see that, option C is the correct answer.

Additional information:
The value of the friction coefficient is usually between 0 to 1. But in some cases, it may be greater than 1. In case of superfluity, its value is zero.

Note: In this type of problems, try to find out different forces in different directions. After that, if required, split them in components along two mutually perpendicular directions. Then equal different forces as required. In this case, since a rope has been considered, we did not need to split any force into components.