Question

A uniform rope of length 5 m is kept on a smooth surface. It is being pulled by a horizontal force of 20 N at one end. Find the ratio of the tension at a distance of 2 m from the force end to the tension at a distance 2 m from the free end.
A) 1 : 1
B) 2 : 3
C) 1 : 2
D) 3 : 2

Answer 1

Hint:Here the rope is pulled by applying a force at one of its ends. Then the acceleration experienced by every point in the rope will be the same. The tension in the rope at any section of the rope will be directed opposite to the force exerted on the rope. The total force acting on a section of the rope will be the difference between the force applied and the tension of that section.

Formula used:
-The total force acting on a rope that is being pulled is given by, $F - T = ma$ where $F$ is the force acting on the rope, $T$ is the tension in the rope, $m$ is the mass of the rope for its entire length and $a$ is the acceleration.

Complete step by step answer.
Step 1: Sketch a rough diagram of the rope being pulled and list the known parameters.

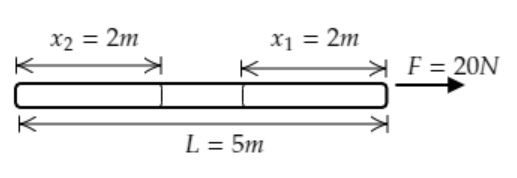
The above figure depicts the rope under consideration.
The length of the rope is given to be $L = 5{\text{m}}$ . A force is applied at one end and it is given to be $F = 20{\text{N}}$ .
Let $m$ be the mass of the rope for its length.
We have to determine the tension ${T_1}$ at a distance ${x_1} = 2{\text{m}}$ from the force end and the tension ${T_2}$ at a distance ${x_2} = 2{\text{m}}$ from the free end.
The acceleration of each point in the rope will be $a = \dfrac{F}{m} = \dfrac{{20}}{m}{\text{m}}{{\text{s}}^{ - 2}}$ .
Step 2: Express the force equation at a distance ${x_1}$ from the force end to find the tension ${T_1}$ .
The total force acting on a rope that is being pulled is given by, $F - T = ma$ ------ (1)
where $F$ is the force acting on the rope, $T$ is the tension in the rope, $m$ is the mass of the rope for its entire length and $a$ is the acceleration.
Consider the section of length 2 m from the force end of the rope as shown in the figure below.

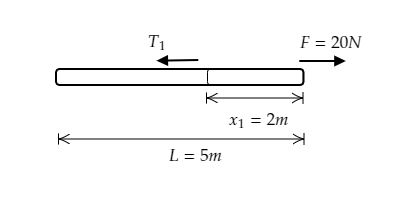
The mass of the rope for its entire length $L = 5{\text{m}}$ is $m$ .
Then the mass of the rope for a length ${x_1} = 2{\text{m}}$ will be ${m_1} = \dfrac{m}{5} \times {x_1} = \dfrac{{2m}}{5}$ .
At a distance ${x_1} = 2{\text{m}}$ from the force end, equation (1) will be $F - {T_1} = {m_1}a$ ------- (2)
Substituting values for $F = 20{\text{N}}$ , ${m_1} = \dfrac{{2m}}{5}$ and $a = \dfrac{{20}}{m}{\text{m}}{{\text{s}}^{ - 2}}$ in equation (2) we get, $20 - {T_1} = \dfrac{{2m}}{5} \times \dfrac{{20}}{m}$
Cancelling the similar terms and simplifying the above equation we get, $20 - {T_1} = 8$ or ${T_1} = 12{\text{N}}$
So the tension at a distance of 2 m from the force end is ${T_1} = 12{\text{N}}$ .
Step 3: Express the force equation at a distance ${x_2}$ from the free end to find the tension ${T_2}$ .
Consider the section of length 2 m from the free end of the rope as shown in the figure below.

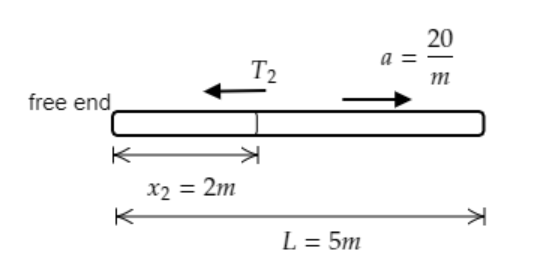
The mass of the rope for its entire length $L = 5{\text{m}}$ is $m$ .
Then the mass of the rope for a length ${x_2} = 2{\text{m}}$ will be ${m_2} = \dfrac{m}{5} \times {x_2} = \dfrac{{2m}}{5}$ .
At the free end, force is zero i.e., $F = 0$.
At a distance ${x_2} = 2{\text{m}}$ from the free end, equation (1) will be ${T_2} = {m_2}a$ ------- (3)
Substituting values for ${m_2} = \dfrac{{2m}}{5}$ and $a = \dfrac{{20}}{m}{\text{m}}{{\text{s}}^{ - 2}}$ in equation (3) we get, ${T_2} = \dfrac{{2m}}{5} \times \dfrac{{20}}{m} = 8{\text{N}}$
So the tension at a distance of 2 m from the free end is ${T_2} = 12{\text{N}}$ .
Step 4: Using the obtained values of ${T_1}$ and ${T_2}$ find the required ratio.
The ration of the tension at a distance of 2 m from the end where force was applied to the tension at a distance of 2 m from the other end of the rope is given by $\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{12}}{8} = \dfrac{3}{2}$ .
So the required ratio is 3 : 2.

Hence the correct option is D.

Note: Alternate method
The tension in a rope of length $L$ at a distance $x$ from the end where a force $F$ is applied is given by, $T = F\left( {\dfrac{{L - x}}{L}} \right)$
At a distance $x = 2{\text{m}}$ from the force end, the tension will be $T = 20\left( {\dfrac{{5 - 2}}{5}} \right) = 12{\text{N}}$
The distance $x' = 2{\text{m}}$ from the free end can be expressed as a distance of $\left( {5 - 2} \right)$ from the force end.
So at a distance 2 m from the free end, the tension will be $T' = 20\left( {\dfrac{{5 - \left( {5 - 2} \right)}}{5}} \right) = 8{\text{N}}$
Now the ratio of the tension at a distance of 2 m from the force end to the tension at a distance 2 m from the free end will be $\dfrac{T}{{T'}} = \dfrac{{12}}{8} = \dfrac{3}{2}$ or 3 : 2.
So the correct option is D.