Question

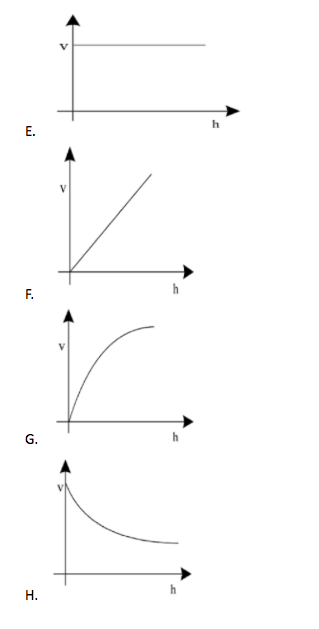
A uniform rope having some mass hangs vertically from a rigid support. A transverse wave pulse is produced at the lower end. The speed of the wave pulse varies with height from the lower end as:

Answer 1

Hint:We can use the formula for the tension generated in the rope. Tension at a some height from bottom$ = $ weight of the rope below it$ = \rho Ahg$
$\rho = $ rope density, A is cross sectional area
Speed of wave$ = \sqrt {\frac{T}{\mu }} $

Step by step solution:
To solve this question we have to calculate the relation between the $v$ and $h$ . To find the relation we can use the formula for the tension and the speed of the wave formula.
Tension in the rope at $h$ from the bottom$ = $ Weight of the rope below it$ = \rho Ahg$
Speed of the wave pulse,$v = \sqrt {\frac{T}{\mu }} $
Putting the value of tension in the above formula.
We get,
$\begin{gathered}
   \Rightarrow v = \sqrt {\frac{{\rho Ahg}}{\mu }} \\
   \Rightarrow v \propto \sqrt h \\
\end{gathered} $
Hence, we can see that the speed is directly proportional to the square root of the height. Hence we can now predict the nature of the graph.
Graph 1 is a constant function, Graph 2 is a straight line graph, Graph 4 is an exponential graph.

Therefore, option C is correct.

Note:While solving this type of question we should have some understanding of the curve tracing concept so that we can easily predict the output graph. We should also be able to get the relationship between the quantities which are to be represented on the graph. We should avoid unnecessary computations to get the answer quickly.