Question

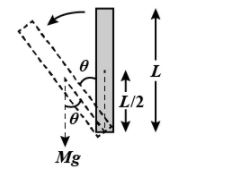
A uniform rod of mass M and length L is pivoted at one end such that it can rotate in a vertical plane. There is negligible friction at pivot. The free end of the rod is held vertically about the pivot and then released. The angular acceleration of the rod when it makes an angle with the vertical is:

Answer 1

Hint: Calculate the torque due to the rotational motion. Calculate the moment of inertia of the rod at the point O. The torque is the force acting on the rod times the perpendicular distance from the axis of rotation.

Formula used:
$\begin{align}
  & \tau =I\alpha \\
 & \tau =F\times S \\
\end{align}$

Complete step-by-step answer:
Let us assume the distance travelled b y the centre of the rods as $S$. The force acting on the rod downward due to the gravitational force is $F=mg$
The torque on the rod due to rotational force will be then,
$\begin{align}
  & \tau =I\alpha \\
 & \tau =\dfrac{M{{R}^{2}}}{3}\alpha \\
\end{align}$
Also, the torque due to the horizontal displacement of the rod will be,
$\begin{align}
  & \tau =FS \\
 & \tau =mg\times \dfrac{L\sin \theta }{2} \\
\end{align}$
Torque in both the cases must be equal so,
$\begin{align}
  & \dfrac{mgL\sin \theta }{2}=\dfrac{m{{L}^{2}}}{3}\alpha \\
 & \alpha =\dfrac{3g}{2l}\sin \theta \\
\end{align}$

Therefore, the angular acceleration of the rod when it makes certain angle with the vertical is $\dfrac{3g}{2l}\sin \theta $

Additional Information: Torque is a force applied to a point on an object about the axis of rotation. It majorly depends on two components, the force applied and the perpendicular distance from the axis of rotation, which is in this case, the vertical axis. A torque must be defined about an axis of rotation. When a torque is applied to an object, it begins to rotate with an acceleration inversely proportional to its moment of inertia. Its relation can also be called Newton's second law of rotation. The moment of inertia is the rotational mass whereas the torque is the rotational force.

Note: Torque must always be defined with respect to an axis of rotation. The S.I unit of torque is N.m which is similar to work done in linear motion. Torque plays an important role in generating power from a car’s engine. The force is measured in pounds per foot in physics.