Question

A uniform rod of mass M and length L is pivoted at one end such that it can rotate in a vertical plane. There is negligible friction at the pivot. The free end of the rod is held vertically above the pivot and then released. What is the angular acceleration of the rod when it makes an angle $\theta $ with the vertical?
$
  {\text{A}}{\text{. g}}\sin \theta \\
  {\text{B}}{\text{. }}\dfrac{{\text{g}}}{{\text{L}}}\sin \theta \\
  {\text{C}}{\text{. }}\dfrac{{{\text{3g}}}}{{2{\text{L}}}}\sin \theta \\
  {\text{D}}{\text{. 6gL}}\sin \theta \\
 $

Answer 1

Hint: Here, we will proceed by drawing the free body diagram of the rod at the inclined angle shown. Then, we will resolve the Mg force acting on the rod into two components (one component passing towards the vertical axis of the rod and the other perpendicular to this vertical axis).
Formulas Used- T = I$\alpha $, Torque produced by force F about any point O = F$ \times $(Perpendicular distance of force F from point O) and I = $\dfrac{{{\text{M}}{{\text{L}}^2}}}{3}$.

Complete Step-by-Step solution:
Let the angular acceleration of the rod when it makes an angle $\theta $ with the vertical be $\alpha $
Given, Mass of the uniform rod = M
Length of the uniform rod = L
Let O be the pivot point of the rod and C be the centre of the rectangular rod
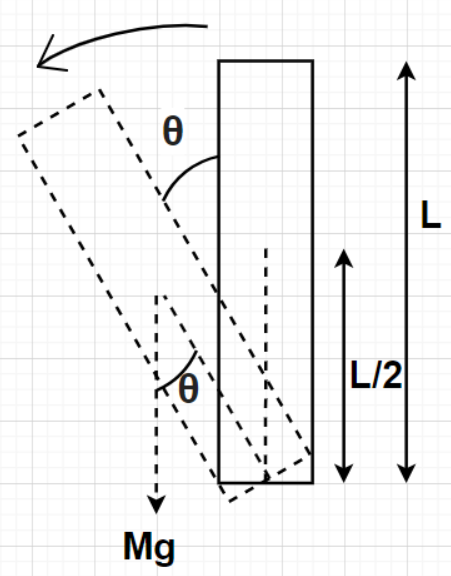
When the rod makes an angle $\theta $ with the vertical, only weight of the rod having mass M acts at the centre of the rod C. This force can be resolved into two components (one component passing towards the vertical axis of the rod and the other perpendicular to this vertical axis) as shown in the figure.
By Newton's second law of motion (angular motion), the sum of the torques produced by external forces acting on the body about any point will be equal to the mass of body times its angular acceleration.
i.e., External torque acting on the body T = I$\alpha $ where I denotes the moment of inertia of the body and $\alpha $ denotes the angular acceleration of the body
For the given uniform rod of mass M, the above formula is given as
External torque acting on the rod about pivot point O, T = I$\alpha {\text{ }} \to {\text{(1)}}$
According to the formula,
Torque produced by force F about any point O = F$ \times $(Perpendicular distance of force F from point O) $ \to (2)$
As we know that the external torque acting on the rod about pivot point O will be equal to the sum of the torque produced by force Mg$\sin \theta $ about pivot point O and the torque produced by force Mg$\cos \theta $ about pivot point O
i.e., External torque acting on the rod about pivot point O = Torque produced by force Mg$\sin \theta $ about pivot point O + Torque produced by force Mg$\cos \theta $ about pivot point O
Using the formula given by equation (2), we get
External torque acting on the rod about pivot point O, T = $\left( {{\text{Mg}}\sin \theta \times {\text{OC}}} \right) + \left( {{\text{Mg}}\cos \theta \times 0} \right) = {\text{Mg}}\sin \theta \times {\text{OC}}$
By putting OC = $\dfrac{{\text{L}}}{2}$ in the above equation, we get
$ \Rightarrow $ T = ${\text{Mg}}\sin \theta \times {\text{OC}}$
$ \Rightarrow $ T = $\left( {{\text{Mg}}\sin \theta } \right) \times \dfrac{{\text{L}}}{2} = \dfrac{{{\text{MgL}}\sin \theta }}{2}$
Also we know that the moment of inertia I of rod having mass M and length L is given by
I = $\dfrac{{{\text{M}}{{\text{L}}^2}}}{3}$
By using T = $\dfrac{{{\text{MgL}}\sin \theta }}{2}$ and I = $\dfrac{{{\text{M}}{{\text{L}}^2}}}{3}$ in equation (1), we get
$
   \Rightarrow \dfrac{{{\text{MgL}}\sin \theta }}{2} = \dfrac{{{\text{M}}{{\text{L}}^2}}}{3}\left( \alpha \right) \\
   \Rightarrow \alpha = \dfrac{{\left( {\dfrac{{{\text{MgL}}\sin \theta }}{2}} \right)}}{{\left( {\dfrac{{{\text{M}}{{\text{L}}^2}}}{3}} \right)}} \\
   \Rightarrow \alpha = \dfrac{{{\text{MgL}}\sin \theta }}{2} \times \dfrac{3}{{{\text{M}}{{\text{L}}^2}}} \\
   \Rightarrow \alpha = \dfrac{{{\text{g}}\sin \theta }}{2} \times \dfrac{3}{{\text{L}}} \\
   \Rightarrow \alpha = \dfrac{{{\text{3g}}}}{{2{\text{L}}}}\sin \theta \\
 $
Therefore, option C is correct.

Note- In this particular problem, the perpendicular distance of the force component Mg$\cos \theta $ from the point O is zero because this force component passes through the point O. Also, the perpendicular distance of the force component Mg$\sin \theta $ from the point O is OC and OC is the equal to half the length of the rod.