Question

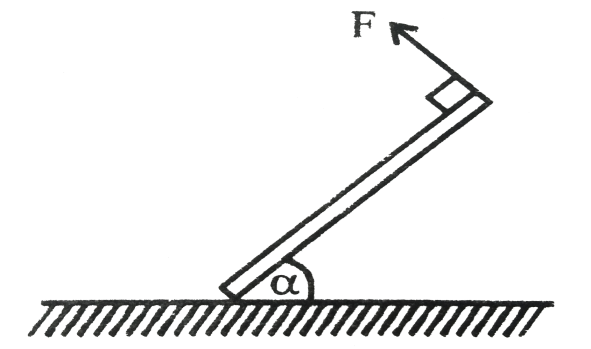
A uniform rod of mass $ m $ and length $ L $ is held at rest by a force $ F $ applied at its end as shown in the vertical plane. The ground is sufficiently rough.
Find
(a) Force $ F $
(b) Normal reaction exerted by the ground
(c) Frictional force exerted by the ground (magnitude and direction)

Answer 1

Hint: The two important forces acting in this question are normal force and frictional force. The normal force is the component of a contact force that is perpendicular to the surface that an object contacts. Friction is the force that resists motion when the surface of one object comes in contact with the surface of another.

Complete step by step solution:
Let $ N $ be the reaction force on the rod by the ground and also let $ C $ be the centre of mass of the rod.
Length of the rod $ = L $
We know that friction $ f = \mu N $
Let us consider two components of the force acting on the rod:
 $ F\cos \alpha $ is the horizontal component of the force $ F $
 $ F\sin \alpha $ is the vertical component of the force $ F $
The equations for translation of rod are
 $ F\cos \alpha = mg - N.........(1) $
 $ F\sin \alpha = \mu N........(2) $
Now, let us consider the equations for the rotational motion about $ Q $
Also, for rotational equilibrium, torque about point $ Q $ should be balance
 $ F\cos \alpha .BD + F\sin \alpha .AD = mg.BE.........(3) $
Here, $ BD = L\cos \alpha $
 $ AD = L\sin \alpha $ $ f = \dfrac{{\mu mg}}{2}(1 + {\sin ^2}\alpha ) $
 $ BE = \dfrac{L}{2}\sin \alpha $
On putting the above values in equation (3),
 $ F\cos \alpha .L\cos \alpha + F\sin \alpha .L\sin \alpha = mg(\dfrac{L}{2}\cos \alpha ) $
 $ FL({\sin ^2}\theta + {\cos ^2}\theta ) = \dfrac{{mgL}}{2}\cos \alpha $
We know that $ {\sin ^2}\theta + {\cos ^2}\theta = 1 $
So, $ FL = \dfrac{{mgL}}{2}\cos \alpha $
 $ F = \dfrac{{mg}}{2}\cos \alpha $
On putting this value in equation (1),
 $ \dfrac{{mg}}{2}{\cos ^2}\alpha = mg - N $
 $ N = \dfrac{{mg}}{2}(2 - {\cos ^2}\alpha ) $
From the identity $ {\sin ^2}\theta + {\cos ^2}\theta = 1 $ , we can write the above equation as
 $ N = \dfrac{{mg}}{2}(1 + {\sin ^2}\alpha )........(4) $
Frictional force $ f = \mu N $
On putting the value of $ N $ from equation (4) in $ f = \mu N $
 $ f = \dfrac{{\mu mg}}{2}(1 + {\sin ^2}\alpha ) $
The direction of this force is towards the right to stop the sliding.

Note:
Any vector in a plane can be resolved in two components. We call the two components horizontal and vertical components. The horizontal component of the vector is given by the cosine of the angle of the vector. Vertical component is given by the sin of the angle of the vector.