Question

A uniform rod of length $l$ is released from rest such that it rotates about a smooth pivot. Find the angular speed of the rod when it becomes vertical.

Answer 1

Hint: So in this question, we have to find the angular speed and for this question as from the question statement we can say that the potential energy will get converted into kinetic energy. Then by using the center of mass theorem and solving the equation we will get to the answer.

Formula used:
The moment of inertia of a rod about its endpoint is given by
$ \Rightarrow I = \dfrac{1}{3}M{l^2}$
Here, $m$ will be the mass of the rod and $l$ will be the length of the rod.

Complete step by step answer
Since the uniform rod of length $l$ is released from rest and it gets rotated about a smooth pivot. So for this, the figure will look like

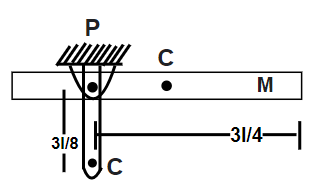
Mass We can see that mass per unit length is $m/l$ .
Therefore, the mass of length $l/4$ will be equal to
$ \Rightarrow \dfrac{l}{4} \times \dfrac{m}{l}$
And on solving it we will get the mass as $\dfrac{m}{4}$ .
Similarly, the mass of length $3l/4$ will be equal to
$ \Rightarrow \dfrac{{3l}}{4} \times \dfrac{m}{l}$
And on solving it we will get the mass as $\dfrac{{3m}}{4}$ .
We also know the moment of inertia of a rod about its endpoint is given by
$ \Rightarrow I = \dfrac{1}{3}M{l^2}$
Therefore, the moment of inertia of $\dfrac{l}{4}$ part will be equal to
  $ \Rightarrow {I_1} = \dfrac{1}{3}\left( {\dfrac{M}{4}} \right){\left( {\dfrac{l}{4}} \right)^2}$
And on solving the above equation, we will get the equation as
$ \Rightarrow {I_1} = \dfrac{{M{l^2}}}{{192}}$
Similarly, the moment of inertia of $\dfrac{{3l}}{4}$ part will be equal to
 $ \Rightarrow {I_2} = \dfrac{1}{3}\left( {\dfrac{{3M}}{4}} \right){\left( {\dfrac{{3l}}{4}} \right)^2}$
And on solving the above equation, we will get the equation as
$ \Rightarrow {I_2} = \dfrac{{9M{l^2}}}{{64}}$
Since from the hint we know that the potential energy will get converted into the kinetic energy, so mathematically it can be written as
$ \Rightarrow P.E = K.E$
Now by using the formula of these two and substituting the values, we will get the equation as
 $ \Rightarrow - \left( {\dfrac{M}{4}} \right)g\left( {\dfrac{l}{8}} \right) + \left( {\dfrac{{3M}}{4}} \right)g\left( {\dfrac{{3l}}{8}} \right) = \dfrac{1}{2}{I_1}{\omega ^2} + \dfrac{1}{2}{I_2}{\omega ^2} $
Now on solving the braces, we will get
 $ \Rightarrow - \dfrac{{mgl}}{{32}} + \dfrac{{9mgl}}{{32}} = \left[ {\left[ {\dfrac{1}{2}\left( {\dfrac{{M{l^2}}}{{192}}} \right) + \dfrac{1}{2}\left( {\dfrac{{9M{l^2}}}{{64}}} \right)} \right]} \right]{\omega ^2} $
On solving further the above equation will become,
 $ \Rightarrow \dfrac{{8mgl}}{{32}} = \left[ {\left( {\dfrac{{M{l^2}}}{{192}}} \right) + \left( {\dfrac{{9M{l^2}}}{{64}}} \right)} \right]\dfrac{{{\omega ^2}}}{2} $
On taking the LCM of it and solving it, we get
 $ \Rightarrow \dfrac{{8mgl}}{{32}} = \left[ {\dfrac{{m{l^2} + 27m{l^2}}}{{192}}} \right]\dfrac{{{\omega ^2}}}{2} $
Solving the above equation again, we get
 $ \Rightarrow \dfrac{{8mgl}}{{32}} = \left[ {\dfrac{{28m{l^2}}}{{192}}} \right]\dfrac{{{\omega ^2}}}{2} $
And by doing the cross multiplication and solving it we get
$ \Rightarrow \omega = \sqrt {\dfrac{{24g}}{{7l}}} $
Therefore, the angular speed of the rod when it becomes vertical $\sqrt {\dfrac{{24g}}{{7l}}} $.

Note:
The center of mass greatly simplifies the problem and helps us analyze its rotational motion, linear motion, skidding, spinning, oscillation, periodic motion, and most other motions quite easily. So that’s why we used the center of mass.