Question

A uniform rod of length $L$ and large $q$ is rotated with a constant angular velocity $\omega $ about an axis passing through its end and perpendicular to its length. Find the magnetic moment associated with its rotation.
A) $\dfrac{1}{{12}}q{L^2}\omega $
B) $\dfrac{1}{{24}}q{L^2}\omega $
C) $\dfrac{1}{3}q{L^2}\omega $
D) $\dfrac{1}{6}q{L^2}\omega $

Answer 1

Hint:When the uniform rod carrying a charge rotates with a constant angular velocity, a current gets generated in the rod. The magnetic moment of the rotation depends on the current generated for the entire rod and the area of the circle described by the rod as it rotates.

Formulas used:
-The magnetic moment of a rotating rod is given by, $M = \int\limits_0^r {dM} $ where $dM$ is the magnetic moment due to a small element of the rod; $dM = dI \cdot A$ where $dI$ is the current through the small element and $A$ is the area of the circle described by it.
-The current generated by the rotation of the small element of charge $dq$ of a rod is given by, $dI = \dfrac{{dq}}{T}$ where $T$ is the period of rotation.
-The period of rotation of a rod is given by, $T = \dfrac{{2\pi }}{\omega }$ where $\omega $ is the constant angular velocity of the rotation.

Complete step by step answer.
Step 1: Sketch a rough figure of the rod to find the current through a small element $dx$.

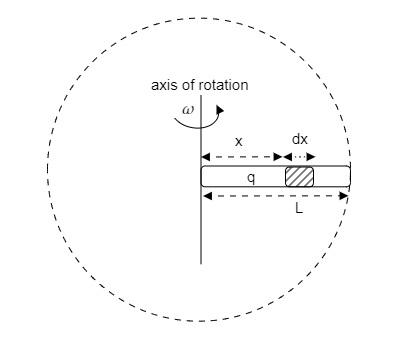
In the above figure, we consider a small element of length $dx$ at a distance $x$ from its axis of rotation. The length of the rod is $L$ and it rotates with a constant angular velocity $\omega $.
The small element carries a charge $dq$ given by, $dq = \dfrac{q}{L}dx$
The current generated by the rotation of the small element will be $dI = \dfrac{{dq}}{T}$ ------ (1) where $T$ is the period of rotation.
Substituting for $dq = \dfrac{q}{L}dx$ and $T = \dfrac{{2\pi }}{\omega }$ in equation (1) we get, $dI = \dfrac{{\left( {\dfrac{q}{L}dx} \right)}}{{\left( {\dfrac{{2\pi }}{\omega }} \right)}}$
Now on simplifying, it becomes $dI = \left( {\dfrac{{q\omega }}{{2\pi L}}dx} \right)$
Thus the current through the small element $dx$ is $dI = \left( {\dfrac{{q\omega }}{{2\pi L}}dx} \right)$ .
Step 2: Express the relation for the magnetic moment of the small element $dx$.
The magnetic moment of a rotating small element of the rod is given by, $dM = dI \cdot A$ -------(2)
where $dI$ is the current generated due to the charge in the small element $dx$ and $A$ is the area of the circle described by the small element as it rotates.
Here, the small element $dx$ describes a circle of radius $x$ and thus the area of the circle will be $A = \pi {x^2}$
Now we substitute for $A = \pi {x^2}$ and $dI = \left( {\dfrac{{q\omega }}{{2\pi L}}dx} \right)$ in equation (2) to get, $dM = \left( {\dfrac{{q\omega }}{{2\pi L}}dx} \right) \times \pi {x^2}$ or on simplifying we get, $dM = \dfrac{{q\omega }}{{2L}}{x^2}dx$ -------- (3).
Step 3: Using equation (3) the magnetic moment of the entire rod is found out.
Equation (3) gives the magnetic moment of the small element $dx$ as $dM = \dfrac{{q\omega }}{{2L}}{x^2}dx$ .
Then to find the magnetic moment $M$ for the entire rod we integrate equation (3) for the length of the rod.
i.e., $M = \int\limits_0^L {dM} $------- (4).
Substituting equation (3) in (4) we obtain $M = \int\limits_0^L {\dfrac{{q\omega }}{{2L}}{x^2}dx} $
On evaluating the integral we get, $M = \dfrac{{q\omega }}{{2L}}\left[ {\dfrac{{{x^3}}}{3}} \right]_0^L$
Then on applying the limit we get, $M = \dfrac{{q\omega }}{{2L}}\left[ {\dfrac{{{L^3}}}{3}} \right] = \dfrac{{q\omega {L^2}}}{6}$
$\therefore $ the magnetic moment of the rod is $M = \dfrac{1}{6}q{L^2}\omega $ .

Hence the correct option is D.

Note:The limits of integration for evaluating the magnetic moment of the entire rod is given varies from $0$ to $L$. This is because the radius of the circle described by the entire rod will be $L$ as the axis of rotation passes through one of the ends of the uniform rod. The limits of integration vary depending on the position of the rotational axis.