Question

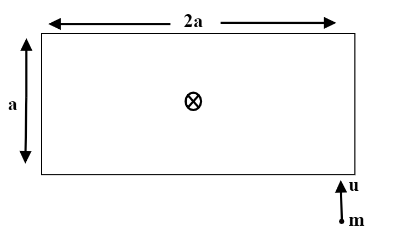
A uniform rectangular plate of mass m which is free to rotate about the smooth vertical hinge passing through the center and perpendicular to the plate is lying on a smooth horizontal surface. A particle of mass m moving with speed 'u' collides with the plate and sticks to it as shown in the figure. The angular velocity of the plate after the collision will be?

A). $ \dfrac{{12u}}{{5a}} $
B). $ \dfrac{{12u}}{{19a}} $
C). $ \dfrac{{3u}}{{2a}} $
D). $ \dfrac{{3u}}{{5a}} $

Answer 1

Hint: The particle of mass m moving with velocity u hits the rectangular plate. The plate will start to rotate in an anticlockwise direction due to the angular momentum which the impact of the particle imparts. This problem can be solved by using the concept of conservation of angular momentum.

Complete Step By Step Answer:
Let $ {L_m} $ be the momentum of the particle of mass m before collision.
 $ {L_m} = a.mu $
Let $ \omega $ be the angular velocity of the rotating system after the collision.
Moment of inertia about a perpendicular axis passing through hinge is given by,
I= moment of inertia of particle of mass m about hinge + moment of inertia of the plate about hinge.
 $ m.\left( {\dfrac{{\sqrt {5a} }}{2}} \right) + \dfrac{1}{{12}}m({a^2} + {(2a)^2}) $
 $ = \dfrac{5}{4}m{a^2} + \dfrac{5}{{12}}m{a^2} $
 $ = \dfrac{{20}}{{12}}m{a^2} $
 $ = \dfrac{5}{3}m{a^2} $
Angular momentum is conserved, therefore
 $ {I_\omega } = {I_p} $
 $ \Rightarrow \dfrac{5}{3}m{a^2}.\omega = mua $
 $ \Rightarrow \omega = \dfrac{{3u}}{{5a}} $
Therefore the angular velocity will be $ \dfrac{{3u}}{{5a}} $ .
The correct answer is option D, $ \dfrac{{3u}}{{5a}} $ .

Note:
Angular velocity, also known as rotational velocity or angular frequency vector, is a vector measure of rotation rate that describes how fast an object spins or revolves in respect to another point, i.e. how fast the angular position or orientation of an object changes over time. During a collision of objects in a closed system, momentum is always conserved.