Question

A uniform meter scale balances at the $40cm$ mark when weights of $10g$ and $20g$ are suspended from the $10cm$ and $20cm$ marks. The weight of the meter scale is:
A. $50g$
B. $60g$
C. $70g$
D. $80g$

Answer 1

Hint: To approach the problem, use the concept of the principle of moments. As it balances the two weights on both sides, this implies that the whole system is in equilibrium. When a system is in equilibrium, the forces acting on the body about the axis of rotation are zero or the torque is zero. Calculate the moments in the clockwise and anticlockwise directions and equate them.

Complete step by step answer:
Suppose, initially the weights were not hanging on the meter scale. So, the scale balances itself at $50cm$ the mark as it is assumed that the scale has a mark from $0cm$ to $100cm$. Let the weight of the scale is $W$ at $50cm$ marking. Now, the weights are put on the scale as shown in the figure. The new mark on which the scale balances itself is $40cm$ .

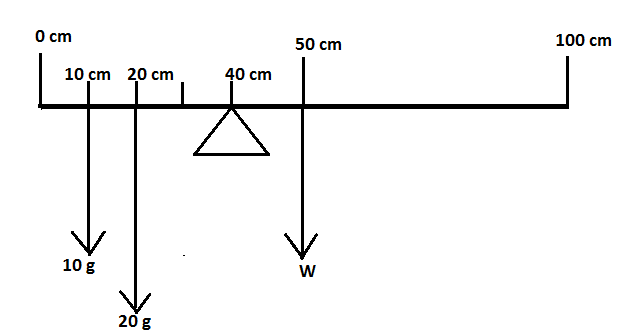
When a system gets balanced at a point, then the sum of clockwise moments about a point is equal to the sum of anticlockwise moments about the same point. This is called the Principle of Moment.
As the scale balances itself at $40cm$marking, the perpendicular distance between $10cm$ marking where the $10g$ weight is suspended and the $40cm$mark is $30cm$ . Similarly, the perpendicular distance between $20cm$ marking where the $20g$ weight is suspended and the $40cm$marking is $20cm$. The perpendicular distance between $50cm$ mark and $40cm$ mark is $10cm$ . Take the right side of the $40cm$ mark to be clockwise and the left side to be anti-clockwise. Here, $40cm$ is the point where the forces are balanced.
Now, the weights given are $10g$ and $20g$ . But, force is a product of mass and acceleration. As the weights are hanging, the acceleration acting on them is due to gravity. The value of acceleration due to gravity is taken as $10m/{s^2}$ approximately. But, we take weights as the force here with unit gram-force as acceleration is also there.
Moments in the clockwise direction $ = 10 \times W......(1)$
Moments in the anti-clockwise direction ${W_1}{d_1} + {W_2}{d_2}$
where ${d_1}\,\& \,{d_2} = $ perpendicular distances
Moments in the anti-clockwise direction $ = 10 \times 30 + 20 \times 20......(2)$
Apply the principle of moments and equate equations (1) and (2), we get:
$10 \times W = 10 \times 30 + 20 \times 20$
$ \Rightarrow \,W = \dfrac{{10 \times 30 + 20 \times 20}}{{10}}$
$ \Rightarrow W = \dfrac{{300 + 400}}{{10}}$
$ \Rightarrow W = \dfrac{{700}}{{10}}$
\[ \therefore \,W = 70\,g\]
Therefore, option (C) is the correct answer.

Note: The moment of a force is defined as the measure of the tendency to cause an object to rotate about a given axis. If the force acts on a body in such a manner that the body would begin to twist, then we can say that moment is developed in a system.
Mathematically, it is defined as the product of the force acting on the body and perpendicular distance between the line of action of the force and the center of moments. It's S.I. unit is Newton-metre (Nm).
Moment, $M = F \times d$
Where $F = $ force in Newton
$d = $ perpendicular distance in meter
From the formula of the moment, we can conclude that the magnitude of the moment is directly proportional to the perpendicular distance of the force from the axis.