Question

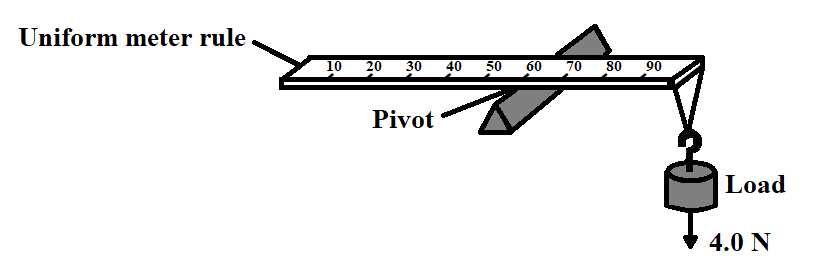
A uniform meter rule of weight $2.0N$ is pivoted at the $60cm$ mark. A $4.0N$ load is suspended from one end, causing the rule to rotate about the pivot. At the instant when the rule is horizontal, what is the resultant moment about the pivot?

$\begin{align}
  & \text{A}\text{. }0.0Nm \\
 & \text{B}\text{. }1.4Nm \\
 & \text{C}\text{. }1.6Nm \\
 & \text{D}\text{. }1.5Nm \\
\end{align}$

Answer 1

Hint: The principle of moment states that an object is in the state of equilibrium if the sum of all anticlockwise moments about the pivot is equal to the sum of all clockwise moments about the same pivot. In case of non-equilibrium points, there should be a net moment on the rule. We will calculate the individual torque due to weight of the rule and the load mass about the pivot. The difference of the two torques acting on the rule, will give the resultant moment about the pivot.

Complete step by step answer:
In the experiment of calculating mass of the meter scale and the net torque acting on it, we use the principle of moments, together with the idea of the centre of gravity.
The centre of gravity of a body is described as a point through which the weight of the body acts, or appears to act. A meter rule has a uniform shape and a constant density and so the centre of gravity is a point lying exactly in the middle of the rule.

The principle of moments states that an object is in the state of equilibrium if the sum of all anticlockwise moments about the pivot is equal to the sum of all clockwise moments about the same pivot. If a meter rule is balanced in a horizontal position at any point, this means that the clockwise moments and the anticlockwise moments must be equal.

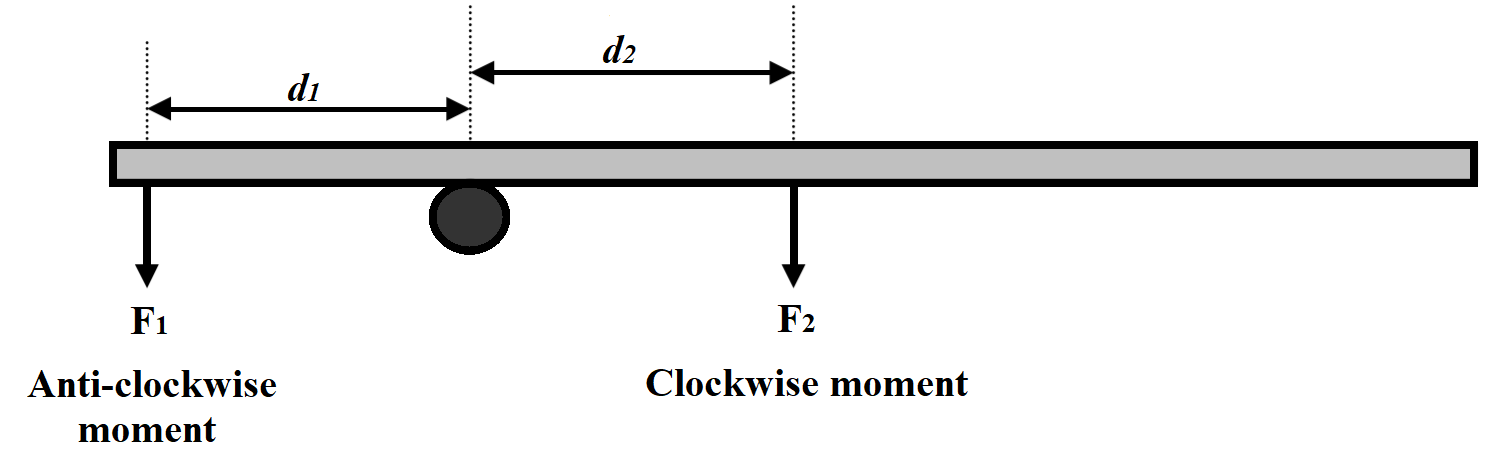
The weight ${F_1}$ of the masses provides the anticlockwise moment and the weight ${F_2}$ of the rule provides the clockwise moment. The weight of the meter rule acts through the point of centre of gravity located at the middle of the rule.
If the meter rule is balanced, we can apply the principle of moments.
We get the equation,
${F_1}{d_1}$ = ${F_2}{d_2}$
Where,
${d_1}$ is the distance between the hanging mass, or load, and the pivot
${d_2}$ is the distance between the pivot and the centre of gravity of the meter rule.
We are given that a uniform meter rule of weight $2.0N$ is pivoted at the $60cm$ mark and a $4.0N$ load is suspended from one end, causing the rule to rotate about the pivot. We need to calculate the net moment acting on the rule about the pivot, when the rule is horizontal.
Torque produced due to the load,
$\Rightarrow \tau_{1} = 4 N \times 0.4m = 1.6Nm $
Torque due to weight of the rule,
$\Rightarrow \tau_{2} = 2 N \times 0.1m = 0.2Nm$
Both the torques are acting in opposite directions, therefore,
Net torque is given as,
$\Rightarrow \tau = 1.6 - 0.2 = 1.4Nm$
The resultant moment about the pivot, when the ruler is in horizontal position is, $1.4Nm$

So, the correct answer is “Option B”.

Note:
For obtaining the balancing point of meter rule, the weight of the rule should be equal to the load mass. In rest of the situations, there will be a net torque on the meter scale due to unbalancing of the weight of pivot and the load. The torque due to meter rule and the torque due to mass load act in opposite directions.