Question

A uniform magnetic field $B = 0.5T$exists in a circular region of radius $R = 5m$.A loop of radius $R = 5m$encloses the magnetic field at $t = 0$and then pulled at uniform speed $V = 2m{s^{ - 1}}$in the plane of the paper. Find the induced emf (in $V$) in the loop at time $t = 3s$.

Answer 1

Hint:We are provided with $B = 0.5T$ $R = 5m$ $t = 0$, $V = 2m{s^{ - 1}}$.And we have to find induced emf at $t = 3s$.For that we had done some changes in our given diagram for our convenience. We had firstly found the length$\left( {PN} \right)$ and then using the formula of induced emf, we solved our problem.

Complete step by step answer:

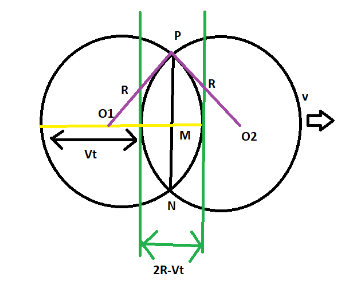
Consider the loop of radius R (shown by purple color) initially at center O1 moving with velocity v. After $t = 3s$the center will move to center O2. Now, we need to find the area travelled i.e. the common part of the two circles which is being represented by the yellow part. To find the yellow part we have to subtract diameter with the distance travelled which can be calculated as
$V = \dfrac{{DISTANCE}}{{TIME}} = \dfrac{D}{t}$
Now calculating length by
In $\Delta {O_1}MP$
${O_1}M = ({V_t} - R) + \dfrac{1}{2}(2R - {V_t})$
$\Rightarrow {O_1}M = \dfrac{1}{2}{V_t}$ $ \ldots \ldots \left( 1 \right)$
As from the above diagram common green part area has total height $PN = 2 \times PM$
For finding the length l$\left( { = PN} \right)$ applying Pythagoras theorem in the above triangle
 $l = 2\sqrt {\left( {{R^2} - {O_1}{M^2}} \right)} $
Using value from $\left( 1 \right)$
$\Rightarrow l = 2\sqrt {({R^2} - {{\left( {\dfrac{{{V_t}}}{2}} \right)}^2})} $
$\Rightarrow l = \sqrt {\left( {4{R^2} - \left( {{V^2}{t^2}} \right)} \right)} $ $ \ldots \ldots \left( 2 \right)$
Now using formula of induced emf $E = Bvl$
By substituting the value from $\left( 2 \right)$
$E = Bv\sqrt {\left( {4{R^2} - \left( {{V^2}{t^2}} \right)} \right)} $
Now using the given values $B = 0.5T$ $v = 2m{s^{ - 1}}$$t = 3s$
$E = 0.5 \times 2\sqrt {4 \times 25 - 4 \times 9} $
$\therefore E = 8V$

Hence, the value of induced emf is $8V$.

Note: Induced emf (electromotive force) which is mainly the potential difference which is being generated by the change in magnetic flux in the circuit. This definition was explained by the famous law i.e., Faraday’s law which states that When the conductor is placed in a varying magnetic field, induced emf is produced in it.