Question

A uniform half meter scale of weight $100\;g$ is balanced at $30\;cm$ point. If $80\;g$ is suspended from one end, where should we suspend a weight at $55\;g$ to bring it in equilibrium?

Answer 1

Hint: Here, we have to assume that the balance is balanced when the moment on the two sides are equal. Here, we need to find the distance at which $55\;g$ must be hung to balance the $80\;g$ which is suspended at one corner of the half meter scale. We can solve the above question as discussed below.

Formula used:
$M=f\times d$

Complete step-by-step solution:
We know that in physics Moments are the measure of the effect made by some torque which acts on the body. And it is expressed mathematically as $M=f\times d$, where is the force applied on the end at the distance $d$ from any fixed axis on the scale.
Given that the total length of the scale is $50\;m$ and it weighs$100\;g$ with the centre of balance at $30\;cm$. Let $55\;g$ be suspended at $x$ on the scale and $80\;g$ on one end say at $0$m, as shown in the figure below

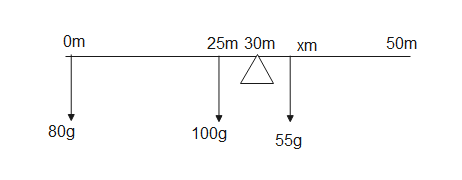
Clearly the mid-point of the scale will have all its wait, then we can say that at $25\;m$ the weight of the scale $100\;g$ will lie.
Consider the moment between the $80\;g$ and $100\;g$, with respect the balance we have
Similarly, Consider the moment between the $55\;g$ and balance at $30\;m$, then the distance of $55\;g$ form balance is $x\;m$, then we have $55(x)$.
Since both must be equal in the couple moment, equating the two we get
$\implies 55x=2900gm$
$\implies x=\dfrac{2900}{55}$
$\therefore x= 52.7m$
This is clearly greater than the half meter of the scale.
Hence we can conclude that we cannot achieve equilibrium.

Note: These moments occur in pairs and are hence called couples also. Since the effect of the moments make the scale here to undergo rotation, we call the applied force to act as a torque to the scale. When the scale is balanced on both the ends, there is no torque and hence the scale is in equilibrium.