
A uniform electric field exists between two charged plates as shown in the figure. What should be the work done in moving a charge q along the closed rectangular path ABCDA.
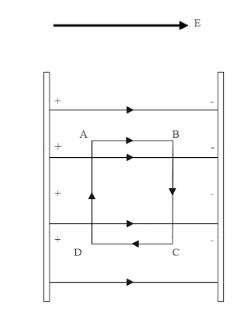

Answer
486.9k+ views
1 likes
Hint: Work done is a property that depends on displacement of the object the force is subjected on.
Formula Used: We will be using the notion that force is conservative and work done by an electric charge
Complete Step by Step solution
We know, in a uniform electric field the field lines are going to move from positively charged plate to the negatively charged one. Now suppose you are placing a charge in between the plates like shown in the figure below. Also consider an imaginary rectangular path ABCD with dimensions,
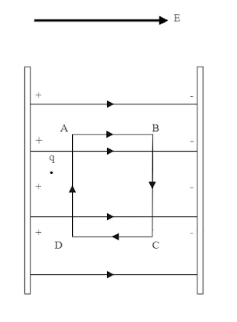
Now let us consider the work done to move the charge from point A to B between the plates.
Here
We also know that,
Similarly, along the path
And thus, the work done to move charge on the path BC,
Similarly for path CD we can see that the angle between the vectors
Also, for the path DA, the angle
Now that we have the work done to move the charge
Thus, the work done is zero. No actual work is done to move a charge around the closed path ABCDA as shown in the figure.
Note
Alternate solution-
Since we can see that the charge is supposed to travel along the path ABCDA. The particle starts from A and ends up back in A, thus making the displacement
Thus, making the work done zero. This simple logic can be used to solve the problem faster.
Formula Used: We will be using the notion that force is conservative and work done by an electric charge
Complete Step by Step solution
We know, in a uniform electric field the field lines are going to move from positively charged plate to the negatively charged one. Now suppose you are placing a charge in between the plates like shown in the figure below. Also consider an imaginary rectangular path ABCD with dimensions,

Now let us consider the work done to move the charge from point A to B between the plates.
Here
We also know that,
Similarly, along the path
And thus, the work done to move charge on the path BC,
Similarly for path CD we can see that the angle between the vectors
Also, for the path DA, the angle
Now that we have the work done to move the charge
Thus, the work done is zero. No actual work is done to move a charge around the closed path ABCDA as shown in the figure.
Note
Alternate solution-
Since we can see that the charge is supposed to travel along the path ABCDA. The particle starts from A and ends up back in A, thus making the displacement
Thus, making the work done zero. This simple logic can be used to solve the problem faster.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Why is insulin not administered orally to a diabetic class 12 biology CBSE

The total number of isomers considering both the structural class 12 chemistry CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?

How do you convert from joules to electron volts class 12 physics CBSE

Define Vant Hoff factor How is it related to the degree class 12 chemistry CBSE

The first microscope was invented by A Leeuwenhoek class 12 biology CBSE




