Question

A uniform disc of radius $R$ is put over another disc of radius $2R$ of the same thickness and density. The peripheries of the two discs touch each other. The position of their center of mass is:
$\left( A \right)$ at$\dfrac{R}{3}$ from the centre of the bigger disc towards the centre of the smaller disc
$\left( B \right)$ at$\dfrac{R}{5}$ from the centre of the bigger disc towards the centre of the smaller disc
$\left( C \right)$ at$\dfrac{2R}{5}$ from the centre of the bigger disc towards the centre of the smaller disc
$\left( D \right)$ at$\dfrac{2R}{5}$ from the centre of the smaller disc towards the centre of the bigger disc

Answer 1

Hint: Here we are given that there are two uniform discs with radius $R$ and $2R$ respectively, having same thickness and density and the peripheries of both discs touch each other. We have to find the position of their center of mass. We will solve this problem using the concept of centre of mass and same mass per unit area as the density and thickness.

Formula used:
Centre of mass formula:
$\left( {{m}_{1}}+{{m}_{2}} \right){{x}_{cm}}={{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}$
Where$\left( {{m}_{1}}+{{m}_{2}} \right)$ is the total mass,
${{x}_{cm}}$ is the effective distance for the total mass (distance to centre of mass)
${{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}$ is the sum of moments of individual masses.

Complete step by step solution:
Let us assume that the centre of the bigger disc is at $\left( 0,0 \right)$. As both discs have the same density and same thickness then their mass per unit area will be the same. Let us say the mass of the bigger disc is ${{M}_{1}}$ and the smaller disc is ${{M}_{2}}$. Therefore, $\dfrac{{{M}_{1}}}{\pi 4{{R}^{2}}}=\dfrac{{{M}_{2}}}{\pi {{R}^{2}}}$ (because radius of first disc is $2R$ and second disc is $R$). From here it comes out to be ${{M}_{1}}=4\times {{M}_{2}}$.
Now, let us find out centre of mass of the system:
Centre of mass of bigger disc will be at $\left( 0,0 \right)$ and centre of mass of smaller disc is at $\left( R,0 \right)$
X component centre of mass $=\dfrac{{{M}_{1}}\times 0+{{M}_{2}}\times R}{{{M}_{1}}+{{M}_{2}}}$by solving this equation we get
${{x}_{cm}}=\dfrac{R{{M}_{2}}}{5{{M}_{2}}}=\dfrac{R}{5}$, this is the location of centre of mass from the centre of bigger disc.

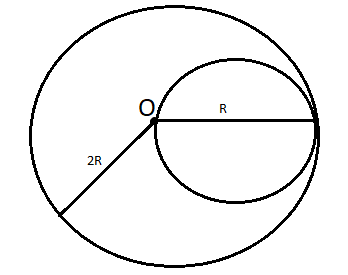
Hence, option $\left( B \right)$ is the correct answer.

Note:
Centre of mass of a system is a unique point of the system where the weighted relative position of the distributed mass sums to zero. One must note that the centre of mass is in between when both the body is equidistant and has the same mass. Here both discs had the same mass but were not equidistant so the centre of mass is not at the middle of both the discs.