Question

A uniform disc of mass $M$ and radius $R$ is mounted on a fixed horizontal axis.A block of mass m hangs from a massless string that is wrapped around the rim of the disk. The magnitude of the acceleration of the falling block (m) is:
A. $\dfrac{{2M}}{{M + 2m}}g$
B. $\dfrac{{2m}}{{M + 2m}}g$
C. $\dfrac{{4M}}{{M + 2m}}g$
D. $\dfrac{{9M}}{{M + 3m}}g$

Answer 1

Hint: In order to solve this question, we use the concept that when block is attached by the string and starts to release down them torque acting on the small block will be produced by tension on the string and balanced by the torque produced by the rotation of uniform disc of mass M and then we will solve for linear acceleration from balancing all the forces acting on smaller block by drawing the free body diagram of the system.

Formula used:
Torque acting on a body due to force F and perpendicular distance r from axis of rotation is
$\tau = F \times r$
Torque due to rotational motion of the body having moment of inertia about axis of rotation I and angular acceleration $\alpha {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} is{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tau = I\alpha $

Complete step by step answer:
Let us first draw the diagram of the system and indicate all forces acting on the smaller object of mass m with tension $T$ acting on the string.

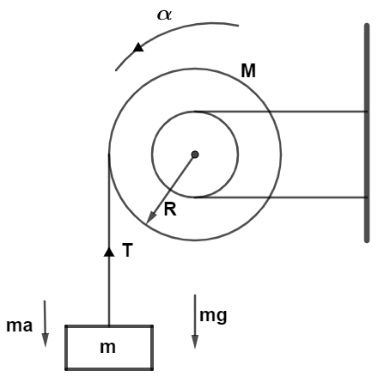
Now, torque on the smaller object of mass $m$ due to this tension on string $T$ and perpendicular distance $R$ (radius of disc) is given by
$\tau = T \times R$
Also, this torque is balanced by torque due to rotation of disc having moment of inertia about the centre axis normally which is given as $I = \dfrac{{M{R^2}}}{2}$ an angular acceleration $\alpha $ is calculated as
$\tau = \dfrac{{M{R^2}}}{2}\alpha $
Equating both torque we get,
$T \times R = \dfrac{{M{R^2}}}{2}\alpha $

Also if linear acceleration of string and smaller bock is a then the we know the relation between angular acceleration and linear acceleration as $\alpha = \dfrac{a}{R}$ put this value in above relation we get,
$T = \dfrac{M}{2}a \to (i)$
Now, from the diagram we can see the forces acting on smaller block then on balancing these forces we can write as,
$T = mg - ma$
Put the value of T from equation (i) in above relation we get,
$\dfrac{M}{2}a = mg - ma$
Solving for a we get,
$a(\dfrac{M}{2} + m) = mg$
$\Rightarrow a(\dfrac{{M + 2m}}{2}) = mg$
$\therefore a = (\dfrac{{2m}}{{M + 2m}})g$

Hence, the correct option is B.

Note: It should be remembered that, the linear acceleration of the point on disc is same as the linear acceleration of string and the smaller object as there are all in linear touch with each other also, moment of inertia of disc is of the axes horizontally passing through the centre of disc and moment of inertia of the disc along the diameter is calculated as $I = \dfrac{{M{R^2}}}{4}.$