Question

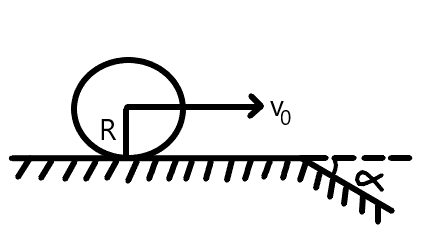
A uniform cylinder of radius rolls over a horizontal plane passing into an inclined plane forming an angle $ \alpha = 30^\circ $ with the horizontal. Find the maximum value of the velocity $ {v_0} $ which still permits the cylinder to roll onto the inclined plane section without a jump. The sliding is assumed to be absent.

Answer 1

Hint :here, we will use the center of mass of the cylinder because it is moving on the plane without sliding. Also, we will use the law of conservation of energy and parallel axis theorem to find the value of the velocity. Here, $ $ {v_0} $ $ will be the maximum velocity that will permit the cylinder to roll onto the cylinder.

Complete Step By Step Answer:
Now, as we know that the cylinder will move without sliding, the center of the cylinder will rotate through the point O, while passing through the common edge of the planes. In other words, the point O will become the foot of the instantaneous axis of rotation of the cylinder.

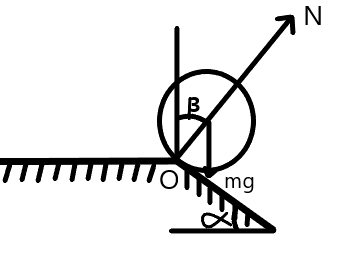
At any instant, let $ {v_1} $ be the velocity of the center of mass of the ring during the sliding of the ring when the angle will be $ \beta $ . Therefore, we have
 $ \dfrac{{mv_1^2}}{R} = mg\cos \beta - N $
Here, let $ N $ be the normal reaction of the edge.
 $ \Rightarrow \,v_1^2 = gR\cos \theta - \dfrac{{NR}}{m} $
Now, from the conservation law of energy, we get
 $ \dfrac{1}{2}{I_0}\dfrac{{v_1^2}}{{{R^2}}} - \dfrac{1}{2}{I_0}\dfrac{{v_0^2}}{{{R^2}}} = mgR\left( {1 - \cos \beta } \right) $
But from the parallel axis theorem, we got the value of $ {I_0} $ which is given below
 $ {I_0} = \dfrac{{m{R^2}}}{2} + m{R^2} = \dfrac{3}{2}m{R^2} $
Now, putting this value of $ {I_0} $ in the above equation, we get
 $ \dfrac{1}{2}\left( {\dfrac{3}{2}m{R^2}} \right)\dfrac{{v_1^2}}{{{R^2}}} - \dfrac{1}{2}\left( {\dfrac{3}{2}m{R^2}} \right)\dfrac{{v_0^2}}{{{R^2}}} = mgR\left( {1 - \cos \beta } \right) $
 $ \Rightarrow \,\dfrac{3}{4}mv_1^2 - \dfrac{3}{4}mv_0^2 = mgR\left( {1 - \cos \beta } \right) $
 $ \Rightarrow \,\dfrac{3}{4}v_1^2 - \dfrac{3}{4}v_0^2 = gR\left( {1 - \cos \beta } \right) $
 $ \Rightarrow \,\dfrac{3}{4}\left( {v_1^2 - v_0^2} \right) = gR\left( {1 - \cos \beta } \right) $
 $ \Rightarrow \,v_1^2 - v_0^2 = \dfrac{4}{3}\left[ {gR\left( {1 - \cos \beta } \right)} \right] $
 $ \Rightarrow \,v_1^2 = v_0^2 + \dfrac{4}{3}\left[ {gR\left( {1 - \cos \beta } \right)} \right] $
Now, equating both the equations of $ v_1^2 $ , we get
 $ v_0^2 = \dfrac{{gR}}{3}\left( {7\cos \beta - 4} \right) - \dfrac{{NR}}{m} $
Here, $ {N_0} $ is the corresponding reaction of the edge.
 $ {v_{\max }} = \sqrt {\dfrac{{gR}}{3}\left( {7\cos \beta - 4} \right) - \dfrac{{NR}}{m}} $
Here, the angle $ \beta $ will be smaller than or equal to $ \alpha $ , therefore, we will replace $ \beta $ by $ \alpha $ . Therefore, the above equation will become
 $ {v_{\max }} = \sqrt {\dfrac{{gR}}{3}\left( {7\cos \alpha - 4} \right) - \dfrac{{NR}}{m}} $
Therefore, the maximum value of the velocity $ {v_0} $ which still permits the cylinder to roll onto the inclined plane section without a jump is $ \sqrt {\dfrac{{gR}}{3}\left( {7\cos \alpha - 4} \right) - \dfrac{{NR}}{m}} $ .

Note :
Here, remember that $ N $ will be greater than $ {N_0} $ . Now, if $ {N_0} $ will be greater than zero than the cylinder will not jump while moving downwards. Thus, we can also say that the value of $ {v_0} $ will be less than $ {v_{\max }} $ .