Question

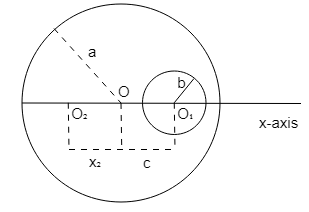
A uniform circular disc of radius \[a\] is taken. A circular portion of radius $b$ has been removed from it as shown in the figure. If the centre of hole is at a distance $c$ from the centre of the disc, the distance ${x_2}$​ of the centre of mass of the remaining part from the initial centre of mass $O$ is given by :

$(A)\dfrac{{\pi {b^2}}}{{{a^2} - {c^2}}}$
$(B)\dfrac{{{b^2}c}}{{{a^2} - {b^2}}}$
$(C)\dfrac{{\pi {c^2}}}{{{a^2} - {b^2}}}$
$(D)\dfrac{{c{a^2}}}{{{c^2} - {b^2}}}$

Answer 1

Hint: In order to solve this question, first we will directly apply the formula for the centre of mass. Then we will put the required values in the expression of the centre of mass. The point $O$ is the centre of the whole disk and is taken as the origin.

Complete step by step solution:
We know the expression for the centre of mass is given by the formula,
${x_{cm}} = \dfrac{{{A_1}{x_1} - {A_2}{x_2}}}{{{A_1} - {A_2}}}......(1)$
Where, ${A_1}$ is the area of the whole disc,
${A_2}$ is the area of the removed part of the disk,
${x_1}$ is the centre of mass of the whole disk,
${x_2}$ is the centre of mass of the removed part of the disk
Now, on putting the values of these quantities, we get,
${A_1} = \pi \times {a^2}$
${A_2} = \pi \times {b^2}$
${x_1} = 0$
${x_2} = c$
On putting the following values in equation (1), we get,
\[{x_{cm}} = \dfrac{{\pi {a^2} \times 0 - \pi {b^2} \times c}}{{\pi {a^2} - \pi {b^2}}}\]
\[{x_{cm}} = \dfrac{{ - \pi {b^2}c}}{{\pi ({a^2} - {b^2})}}\]
On cancelling the value of $\pi $ on both the sides, we get,
\[{x_{cm}} = \dfrac{{ - {b^2}c}}{{({a^2} - {b^2})}}\]
The negative sign in the above expression shows that the centre of mass is present on the left and side.
So, we can conclude that from the point $O$, the centre of mass is present in the left hand side at a distance of \[\dfrac{{{b^2}c}}{{({a^2} - {b^2})}}\].
So, the final answer is $(B)\dfrac{{{b^2}c}}{{{a^2} - {b^2}}}$.

Note:
It is important to note that the centre of mass can be negative as well as positive. If the centre of mass is negative, then it means that the centre of mass is present on the left hand side and if it is positive, then it means that it is present on the right hand side. Also, the centre of mass of a body can lie outside the body. For example, the centre of mass of any particular ring lies at its centre but the centre itself is not a part of the ring.