Question

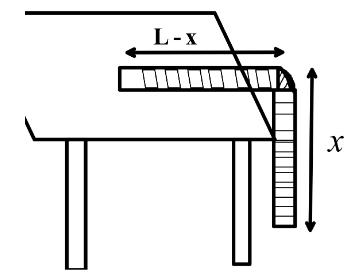
A uniform chain of mass m and length \[L\] is kept on the table with a part of it overhanging (see figure). If the coefficient of friction between the table and the chain is \[\dfrac{1}{3}\] then find the maximum length of the chain that can overhang such that the chain remains in equilibrium.

A. \[\dfrac{L}{3}\]
B. \[\dfrac{L}{2}\]
C. \[\dfrac{L}{4}\]
D. \[\dfrac{{2L}}{3}\]

Answer 1

Hint: To solve this problem find the forces acting on the chain overhanging and the chain on the table to find the maximum length of the chain that can overhang such that the chain remains in equilibrium. The force acting on the chain on the table is friction force. The force on the part of the chain overhanging is gravitational force. Friction force of a surface with coefficient of friction \[\mu \], is given by, \[f = \mu N\] where \[N\] is the normal force given by the table.

Complete step by step answer:
Here, we can see that to remain at rest the force must be equal to zero. Now, the force acting on the hanging part of the chain is the gravitational force and the force acting on the part of the chain that is on the table is frictional force. So, for equilibrium these two forces must be equal.

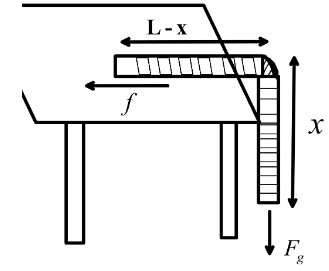
Now, we know that the frictional force of a surface with coefficient of friction \[\mu \], is given by, \[f = \mu N\] where \[N\] is the normal force given by the table. Now, we have given here the total length of the chain is \[L\] , length overhanging is \[x\]. So, the length of the part of the chain that is on the table is \[L - x\].

Now, Let’s say the mass per unit length of the chain is \[m\] and the total mass of the chain is \[M = mL\]. So, the mass of the chain that is on the table is \[m(L - x)\]. Mass of the chain overhanging is \[mx\]. Now, the frictional force on the chain on the table is, \[f = \mu m(L - x)g\]. We have given, \[\mu = \dfrac{1}{3}\].Putting the value in the equation we get,
\[f = m\dfrac{1}{3}(L - x)g\]

Now, the gravitational force acting on the overhanging part is,
\[F = mxg\]
So, to remain at equilibrium these two forces must be equal. Hence, we get,
\[mxg = m\dfrac{1}{3}(L - x)g\]
\[ \Rightarrow x = \dfrac{1}{3}(L - x)\]
\[\Rightarrow 3x = L - x\]
Simplifying we get,
\[4x = L\]
\[\Rightarrow x = \dfrac{L}{4}\]
Since, the maximum value of frictional force is \[f = m\dfrac{1}{3}(L - x)g\]. So, the maximum length of the chain that can overhang is \[\dfrac{L}{4}\].

Hence, the correct answer is option C.

Note: The mass per unit length must be uniform else here, we would not be able to solve for an answer. When the gravitational force is greater than the frictional force that means when the overhanging length is greater than \[\dfrac{L}{4}\]the chain drops to the ground with increasing acceleration until its left the table after that it drops with the acceleration as same as the gravitational acceleration \[g\].