Question

A uniform bar $PO$ is 1 m long. from the end $P$, two masses of 20 g and 50 g are hung at distances of 10 cm and 30 cm respectively. If the weight of the bar is 100 g, find the position of the point where the bar will balance horizontally.

Answer 1

Hint: Use the condition for equilibrium to find the position of the point where the bar will balance horizontally. The bar will balance where the net torque acting on the system is equal to zero. Torque is equal to the product of force times the perpendicular distance between the force acting.

Complete step by step answer:
We have given here that, a uniform bar PO is 1 m long, from the end P, two masses of 20 g and 50 g are hung at distances of 10 cm and 30 cm respectively. The weight of the bar is 100 g. We have to find the position of the point where the bar will balance horizontally.

Now, to balance the bar the net torque must be equal to zero. Let the bar balance at a point $x$ cm of the bar from mid-point. Now, The torque due to the whole system is the weight of the system times the balancing position. And torque due to each of the masses is equal to the weight times the distance.

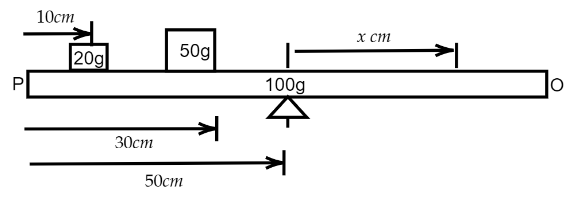
So, the torque equation becomes,
\[{W_1}{l_1} + {W_2}{l_2} + {W_3}{l_3} = {W_{1,2,3}}x\]
Putting the values, \[{W_1} = 20g\], \[{W_2} = 50g\], \[{W_3} = 100g\], position from the midpoints, \[{l_1} = 50 - 10 = 40cm\] , \[{l_2} = (50 - 30) = 20cm\] \[{l_3} = 0\] we will have,
\[20g \times 40 + 50g \times 20 + 100g \times 0 = (100 + 50 + 20)gx\]
\[\Rightarrow 1800\,g = 170g.x\]
\[\Rightarrow x = \dfrac{{1800g}}{{170g}}\]
\[\Rightarrow x = 10.58\,cm\]
So, from the midpoint the distance is at \[10.58\,cm\]. So, from end O the point will be at a distance of, \[x = (50 - 10.58) = 39.4\,cm\]

So, the bar will balance horizontally at a distance of \[39.4\,cm\] from the end O.

Note: The torque due to a force is given by, \[\tau = \vec r \times \vec F\]. Here, since the weight and the distance is always perpendicular to each other, we have used the magnitude of torque as, \[\tau = rF\]. Also, note that the balancing point is at a position greater than the midpoint or at the other side of the bar.