Question

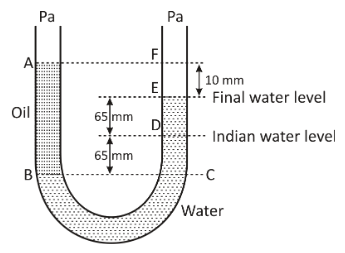
A U tube with both the end open to the atmosphere, is partially filled with water, oil, which is immiscible with water, is poured into one side until it stands at a distance of \[10\,{\text{mm}}\] above the water level on the other side. Meanwhile the water rises by \[65\,{\text{mm}}\] from its original level (see diagram). The density of the oil is:

A. \[928\,{\text{kg}}\,{{\text{m}}^{ - 3}}\]
B. \[650\,{\text{kg}}\,{{\text{m}}^{ - 3}}\]
C. \[425\,{\text{kg}}\,{{\text{m}}^{ - 3}}\]
D. \[800\,{\text{kg}}\,{{\text{m}}^{ - 3}}\]

Answer 1

Hint: First of all, we will find out the height of the water column and the column of oil. Then we will apply the concept that pressure on both the sides must be equal in order to keep liquids in both the arms in an equilibrium position. We will manipulate the expression accordingly and find the result.

Formula used:
The applied pressure is given by the formula given below:
\[p = \rho \times g \times h\] …… (1)
Where,
\[p\] indicates the applied pressure.
\[\rho \] indicates the density of the liquid.
\[g\] indicates the acceleration due to gravity.
\[h\] indicates the height of the liquid column.

Complete step by step answer:
In the given question, we are supplied with the following data:
There is a U shaped tube in which both the ends are open to the atmosphere. In the left arm, there is filled with oil, while in the right arm, it is filled with water. The oil column stands at a distance of \[10\,{\text{mm}}\] above the water level on the other side.The initial water level was \[65\,{\text{mm}}\] but after the oil was poured into the tube, it again rose by \[65\,{\text{mm}}\] . We are asked to determine the density of the oil.

To begin with, let us first assume the line \[BC\] as the base line. We will measure the height of the two liquid columns from that level. As we can clearly see that the height of the water \[{h_{\text{w}}}\] is \[CE\] . Now we write:
${h_{\text{w}}} = CD + DE \\
\Rightarrow {h_{\text{w}}} = 65 + 65 \\
\Rightarrow {h_{\text{w}}} = 130\,{\text{mm}} \\$
Again, we calculate the height of the column containing the oil.
We write as:
${h_{\text{o}}} = BA \\
\Rightarrow {h_{\text{w}}} = CD + DE + EF \\
\Rightarrow {h_{\text{w}}} = 65 + 65 + 10 \\
\Rightarrow {h_{\text{w}}} = 140\,{\text{mm}} \\$
We know that the pressure on both sides will be equal, as the position of both the liquids are in equilibrium. So, we can equate the applied pressure of both the oil and the water column.
${\rho _{\text{w}}} \times g \times {h_{\text{w}}} = {\rho _{\text{o}}} \times g \times {h_{\text{o}}} \\
\Rightarrow 1000 \times 130 = {\rho _{\text{o}}} \times 140 \\
\Rightarrow {\rho _{\text{o}}} = \dfrac{{130}}{{140}} \times 1000 \\
\Rightarrow {\rho _{\text{o}}} = 928\,{\text{kg}}\,{{\text{m}}^{ - 3}} \\$
Hence, the density of oil is \[928\,{\text{kg}}\,{{\text{m}}^{ - 3}}\] .

The correct option is A.

Note: This problem is based on the principle of manometer. While solving this problem, it is important to remember that higher is the density, lower is the height, if we apply a constant pressure, comparing two different liquids. The liquid in the manometer only stops moving when the pressure exerted on one side is equal to the pressure on the other side.