Question

A T.V transmitting antenna is 128m tall. If the receiving is at ground level, the maximum distance between them for satisfactory communication in L.O.S mode is:
(Radius of earth=$6.4\times {{10}^{6}}m$)
\[A.\quad 64\times \sqrt{10}km\]
\[B.\quad \dfrac{128}{\sqrt{10}}km\]
\[C.\quad 128\times \sqrt{10}km\]
\[D.\quad \dfrac{64}{\sqrt{10}}km\]

Answer 1

Hint: As per the basics of communication, the maximum distance (d) for satisfactory transmission between two antennas, with one at height (h) and the other at ground level is $d=\sqrt{2rh}$.
Here r stands for the radius of earth.

Step by step solution:
Given in the problem, we have an antenna of perpendicular height of 128m, that is (h=128m). This antenna is on the surface of earth. The earth’s radius is given to be 6400km, that is (R=$6.4\times {{10}^{6}}m$). This antenna at the height of 128m can transmit signals for communication up to distance (d). Hence, at distance (d) from the antenna at height (h) a receiving antenna is set up at the ground level.

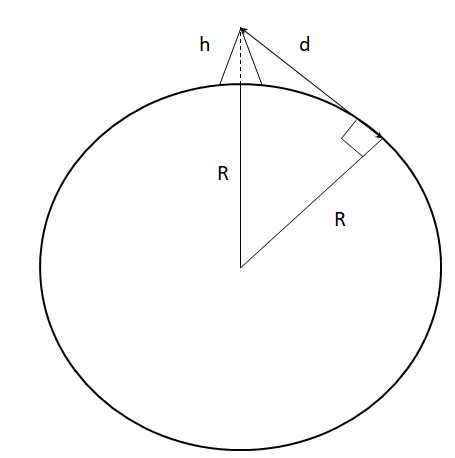
The maximum distance from the antenna at height (h) to the ground based antenna at distance (d) is given by the formula $d=\sqrt{2Rh}$ , for the L.O.S transmission can be derived from the Pythagorean theorem.

${{d}^{2}}+{{R}^{2}}={{(R+h)}^{2}}\Rightarrow {{d}^{2}}={{(R+h)}^{2}}-{{R}^{2}}\Rightarrow {{d}^{2}}=2Rh+{{h}^{2}}$.

However, since, the value of $({{h}^{2}})$ is much smaller than 2Rh, hence it can be neglected against 2Rh. Therefore, the value of d becomes, $d=\sqrt{2Rh}$.

Therefore, substituting in the values of r=$6.4\times {{10}^{6}}m$and value of h=128m above, we get, $d=\sqrt{2(6.4\times {{10}^{6}}m)(128m)}\Rightarrow d=\dfrac{128}{\sqrt{10}}\times {{10}^{3}}m$.

Hence, the maximum distance between the antenna at the height and the one at the ground level for satisfactory communication is $d=\dfrac{128}{\sqrt{10}}km$.

Note:
It is important to remember that L.O.S which stands for line of sight is the kind of communication over here. Hence, in this kind of communication a direct straight line based communication happens and if any obstacle obstructs or comes in between the two antennas, the communication won’t occur.
For the case when there are obstacles between two antennas, then reflection of communication signals is used which requires additional antennas in between to reflect and change the direction of signals to relay the information.