Question

A turn of radius $20m$ is banked for the vehicles going at a speed of $36km/h$. If the coefficient of static friction between the road and the tyre is $0.4$, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
A) $14.7km/h$ and $54km/h$
B) $14.2km/h$ and $50km/h$
C) $11.7km/h$ and $44km/h$
D) $17.7km/h$ and $34km/h$

Answer 1

Hint:In this question we want to find the range of speed of vehicle so that it neither slip down nor skids up
We take two possible conditions when a vehicle moving its maximum speed means if it increases its speed now it will skid up. In this condition we mark all forces and balance them and same thing we will do for minimum speed friction gives required centripetal force for turn

Complete step by step answer:
In the question it is given radius of turn $r = 20m$ and banked with angle $\theta $ for speed $v = 36km/h = \dfrac{{36 \times 5}}{{18}} = 10m/\sec $
And coefficient of friction $\mu = 0.4$
From here we can find the value of $\tan \theta $
We know $\tan \theta = \dfrac{{{v^2}}}{{rg}}$
$ \Rightarrow \tan \theta = \dfrac{{{{10}^2}}}{{20 \times 10}} = \dfrac{1}{2}$ .............. (1)
We assume two conditions one when a vehicle moves with maximum speed in this condition the vehicle may skid up if speed will increase.
In this situation friction between road and tyre is opposite to skidding direction as shown in figure
We mark all forces on vehicle as shown in figure and dividing them in their component
From figure clearly see that if vehicle is in equilibrium so the force acting on vehicle are equal along the road and perpendicular to the road
Force along the road

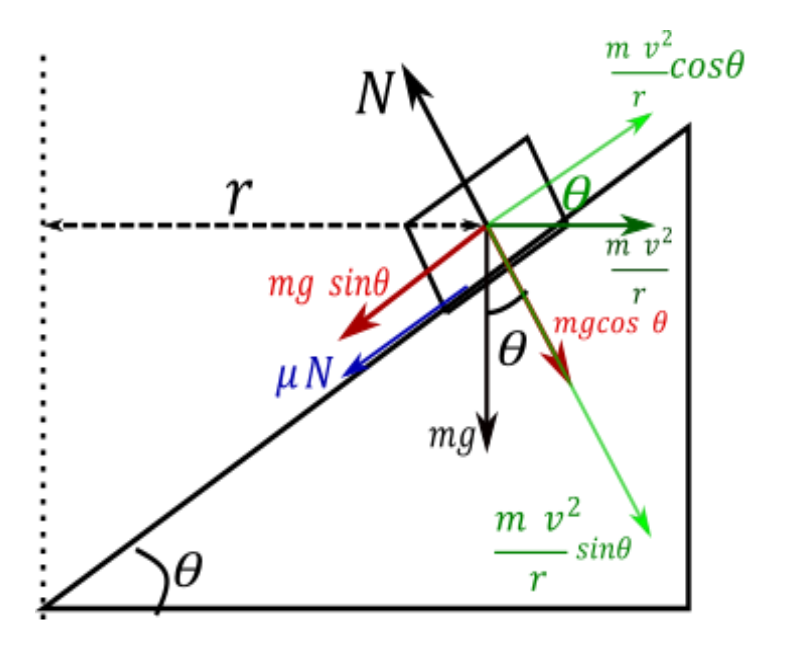
$ \Rightarrow mg\sin \theta + \mu N = \dfrac{{m{v^2}}}{r}\cos \theta $
Rearranging this equation
$ \Rightarrow \mu N = \dfrac{{m{v^2}}}{r}\cos \theta - mg\sin \theta $ ............ (2)
Now take forces perpendicular to road
$ \Rightarrow N = mg\cos \theta + \dfrac{{m{v^2}}}{r}\sin \theta $ ............... (3)
Divide (2) by (3)
$ \Rightarrow \mu = \dfrac{{\dfrac{{m{v^2}}}{r}\cos \theta - mg\sin \theta }}{{mg\cos \theta + \dfrac{{m{v^2}}}{r}\sin \theta }}$
Solving this equation we get
$ \Rightarrow \mu = \dfrac{{{v^2}\cos \theta - r\sin \theta }}{{rg\cos \theta + {v^2}\sin \theta }}$
Right hand side divided by $\cos \theta $
$ \Rightarrow \mu \left( {rg + {v^2}\tan \theta } \right) = {v^2} - rg\tan \theta $
Solving this we can find value of $v$ maximum velocity of vehicle where it will not skid
$ \Rightarrow v = \sqrt {\dfrac{{rg\tan \theta + \mu rg}}{{1 - \mu \tan \theta }}} $
Put the given values in this equation
$ \Rightarrow v = \sqrt {\dfrac{{20 \times 10 \times \dfrac{1}{2} + 0.4 \times 20 \times 10}}{{1 - 0.4 \times \dfrac{1}{2}}}} $
$ \Rightarrow v = \sqrt {225} $
$v = 15m/\sec $
Convert into $km/h$
Maximum speed $v = 54km/h$
Now we take the minimum speed case in this case friction applied in upward direction along the road as shown in figure.

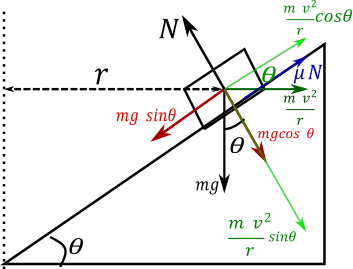
Equate Forces along road
$ \Rightarrow \mu N + \dfrac{{m{v^2}}}{r}\cos \theta = mg\sin \theta $
$ \Rightarrow \mu N = mg\sin \theta - \dfrac{{m{v^2}}}{r}\cos \theta $ .................. (4)
Forces perpendicular to road
$ \Rightarrow N = mg\cos \theta + \dfrac{{m{v^2}}}{r}\sin \theta $ ............... (5)
Divide (4) by (5)
$ \Rightarrow \mu = \dfrac{{mg\sin \theta - \dfrac{{m{v^2}}}{r}\cos \theta }}{{mg\cos \theta + \dfrac{{m{v^2}}}{r}\sin \theta }}$
Solving this we get
$ \Rightarrow \mu = \dfrac{{rg\sin \theta - {v^2}\cos \theta }}{{rg\cos \theta + {v^2}\sin \theta }}$
Divide right hand side by $\cos \theta $
$ \Rightarrow \mu = \dfrac{{rg\tan \theta - {v^2}}}{{rg + {v^2}\tan \theta }}$
Further solving it we get
$ \Rightarrow v = \sqrt {\dfrac{{rg\tan \theta - \mu rg}}{{\mu \tan \theta + 1}}} $
Putting given values in above equation
$ \Rightarrow v = \sqrt {\dfrac{{20 \times 10 \times \dfrac{1}{2} - 0.4 \times 20 \times 10}}{{0.4 \times \dfrac{1}{2} + 1}}} $
By solving this
$ \Rightarrow v = \sqrt {16.66} $
Minimum speed
$\therefore v = 4.08m/\sec $
Convert into $km/h$
$v = 4.08 \times \dfrac{{18}}{5} = 14.68km/h$
Hence the minimum speed is $14.7km/h$

Hence in this question option A is correct

Note:We get the range of speed of vehicle is $14.7km/h$ to $54km/h$ its means that if vehicle moves with slower speed then $14.7km/h$ than it will slip down because friction in upward direction can not provide sufficient centripetal force to take turn
And if a vehicle moving with higher speed then $54km/h$ then the friction force can not provide centripetal force to hold the vehicle so it will skid up.