Question

A tunnel is made across the earth passing through its centre. A ball is dropped from a height h in the tunnel. The motion will be periodic with time period:
A) $2\pi \sqrt {\dfrac{R}{g}} + \sqrt {\dfrac{{2h}}{g}} $
B) $2\pi \sqrt {\dfrac{R}{g}} + 4\sqrt {\dfrac{h}{g}} $
C) $2\pi \sqrt {\dfrac{R}{g}} + 4\sqrt {\dfrac{{2h}}{g}} $
D) $2\pi \sqrt {\dfrac{R}{g}} + \sqrt {\dfrac{h}{g}} $

Answer 1

Hint:In order to solve this question a student must always keep in mind that whatever may be the position of an object is, the force as well as the acceleration due to gravity will always be having a direction always towards the centre of the earth. Using this concept we can derive the time period for the ball in the given problem.

Complete step by step answer:

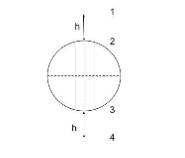
The ball is dropped from a point 1 at a height h above the surface. Thus during the entire motion, let the time taken by the ball to move move from 1 to 2 be t₁, from 2 to 3 and 3 to 2 be t₂, from 3 to 4 be t₃
, from 4 to 3 be t₄​, and from 2 to 1 be t₅
​ Let T be the time period of the complete motion.
Hence, for the motion from 1 to 2, we can write
$h = 0 + \dfrac{1}{2}gt_1^2$ $ \to {t_1} = \sqrt {\dfrac{{2h}}{g}} $
Similarly, we can write,
${t_3} = {t_4} = {t_5} = {t_1} = \sqrt {\dfrac{{2h}}{g}} $
The time period for executing the simple harmonic motion inside the tunnel is given by
$t = 2\pi \sqrt {\dfrac{R}{g}} $
Hence, the time period inside the tunnel i.e from 2 t 3 and 3 to 2 can be written as,
${t_2} = 2\pi \sqrt {\dfrac{R}{g}} $
Now, the total periodic time (T) is given by
$T = {t_1} + {t_2} + {t_3} + {t_4} + {t_5}$
Therefore,
$T = 2\pi \sqrt {\dfrac{R}{g}} + 4\sqrt {\dfrac{{2h}}{g}} $

Hence, option C is the correct choice.

Note:The main concept behind the derivation is that the acceleration due to gravity changes as the position of a body with respect to the centre of the earth changes. It is advisable to go through all such derivations for solving such problems.