Question

A tuning fork with frequency $800\;Hz$ produces resonance in a resonance column tube with upper end open and lower end closed by water surface. Successive resonances are observed at lengths 9.75 cm, 31.25 cm and 52.75 cm. The speed of sound in air is:
A. $172\;ms^{-1}$
B. $500\;ms^{-1}$
C. $156\;ms^{-1}$
D. $344\;ms^{-1}$

Answer 1

Hint: Recall the expression for the resonant frequency of a tube with one closed end. This expression will relate the frequency to the number of harmonics, the speed of sound and the length of the tube at which the resonance is obtained. Rearrange the equation to express resonance lengths of the tube in terms of all the other parameters in the expression. Then, keeping in mind that the resonance tube forms only odd harmonics, rewrite the obtained equations in such a way that you can equate them to consequently obtain the speed of sound.

Formula used: Resonance frequency $f = \dfrac{nv}{4l}$

Complete step by step answer:
We know that acoustic resonance is a phenomenon wherein an acoustic system amplifies the sound waves whose frequency matches its own natural frequency of vibration.
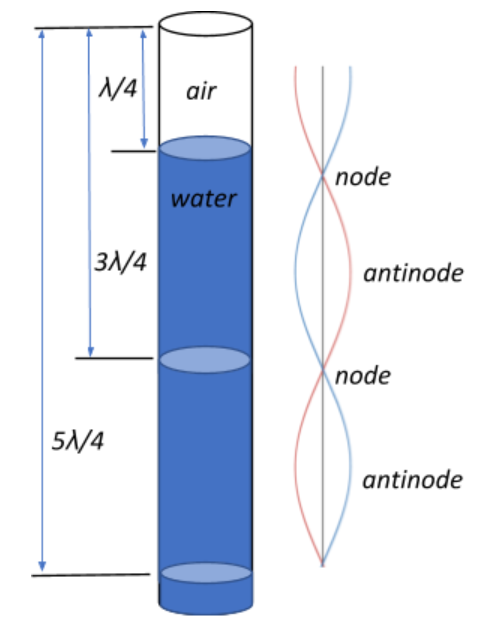
A resonance tube with the lower end closed by water surface will have resonances at frequencies
$f = \dfrac{nv}{4l}$, where n is an odd positive integer, v is the speed of sound, and l is the length of the resonant tube.This tube produces only odd harmonics.
Let the frequency of the tuning fork be $f_{fork}$, and let the successive lengths at which resonances are observed be at $l_1,\; l_2,\;$ and $l_3$ respectively. Then, we have:
$f_{fork} = \dfrac{nv}{4l_1} \Rightarrow l_1 = \dfrac{nv}{4f_{fork}}$
$f_{fork} = \dfrac{(n+2)v}{4l_2} \Rightarrow l_2 = \dfrac{(n+2)v}{4f_{fork}}$, and
$f_{fork} = \dfrac{(n+4)v}{4l_3}$, since only odd harmonics are produced, i.e., at n, n+2, and n+4, since n is an odd positive integer.
Subtracting the equations of the first two harmonics
$l_2 – l_1 = \dfrac{(n+2)v}{4f} - \dfrac{nv}{4f} = \dfrac{2v}{4f} = \dfrac{v}{2f}$
In the question, we are given that $l_1 = 9.75\;cm$ and $l_2 = 31.25\;cm$ and $f_{fork} = 800\;Hz$
$\Rightarrow (31.25 – 9.75) \times 10^{-2} = \dfrac{v}{2\times 800} $
$\Rightarrow v = 21.5 \times 10^{-2} \times 1600 = 344\;ms^{-1} $

So, the correct answer is “Option D”.

Note: Remember that the expression for resonances of the resonance tube vary depending on the structure of the tube. The expression we used is only applicable for that tube that is closed on one end, and for open tubes it will thus be: $f = \dfrac{nv}{2l}$.
Also, the resonance properties of a resonance tube can be understood by considering the behaviour of a sound wave in air, which propagates via the compressions and rarefactions of the molecules of the medium. Within a tube, a standing wave is formed, with the closed end being the displacement node or the point of no vibration.