Question

A tube is mounted so that it’s base is at height $'h'$above the horizontal ground. The tank is filled with water to a depth $h$. A hole is punched in the side of the tank at depth $y$ below the water surface. Then the value of $y$ so that the range of the emerging stream would be maximum?
A. $h$

B. $\dfrac{h}{2}$

C.$\dfrac{h}{4}$

D. $\dfrac{3h}{4}$

Answer 1

Hint: Draw proper diagram. Convert word problems into equations and use the equation of laws of motion to solve it.
Formula used: $s = ut + \dfrac{1}{2}a + 2$
${v^2} = {u^2} = 2as$

Complete step by step answer:

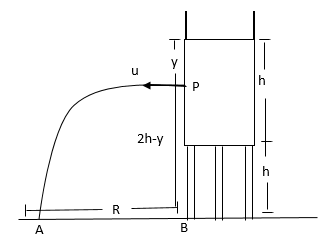
Let a tube be mounted at height $h$from the ground.
Then, it is filled by water to a height, $h$.
Then , a hole is punched in the side of the tank at depth $y$below the water surface.
Let the water coming out of the hole fall in the form of stream at point $A.$
Then distance $AB$is the range $R.$
Let $P$be the point where the hole is punched.
$ \Rightarrow PB = 2h - y$
From the Newton’s laws of motion,
We know that
$s = ut + \dfrac{1}{2}a{t^2}$
$ \Rightarrow 2h - y = 0 + \dfrac{1}{2}g{t^2}$
Vertical velocity is zero in case of horizontal projectile.
Rearranging the equation, we get
${t^2} = \dfrac{{2\left( {2h - y} \right)}}{g}$
$t = \sqrt {\dfrac{{2\left( {2h - y} \right)}}{g}} $
 Now, since range is the horizontal distance, and distance$ = speed \times time$
We can write,
$R = u \times t$ . . . . . (1)
Now, we know that
${v^2} = {u^2} = 2as$
For horizontal velocity of projectile final velocity is zero.
$ \Rightarrow - {u^2} = 2as$
Also, $a = g$and $s = - y$
$ \Rightarrow - {u^2} = 2g\left( { - y} \right)$
$ \Rightarrow {u^2} = 2gy$
$ \Rightarrow u = \sqrt {2gy} $
Put the value of $u$and $t$in equation (1) to calculate $R.$
$ \Rightarrow R = \sqrt {2gy} \times \sqrt {\dfrac{{2\left( {2h - y} \right)}}{g}} $
Multiplying, we get
$R = 2\sqrt {\dfrac{{gy\left( {2h - y} \right)}}{g}} $
$ \Rightarrow R = 2\sqrt {y\left( {2h - y} \right)} $
Now, $R$is maximum if
$\dfrac{{dR}}{{dy}} = 0$ and $\left( {\dfrac{{{d^2}R}}{{d{y^2}}}} \right) < 0$
$ \Rightarrow \dfrac{{dR}}{{dy}} = \dfrac{d}{{dy}}\left[ {2\sqrt {y(2h - y)} } \right]$
$ = 2\dfrac{d}{{dy}}\sqrt {2hy - {y^2}} $
$ = 2\dfrac{1}{{\sqrt {2hy - {y^2}} }}\dfrac{d}{{dy}}\left( {2hy - {y^2}} \right)$
$\left( {\because \dfrac{d}{{dx}}{x^n} = n{x^{n - 1}}} \right)$
$ = \dfrac{2}{{\sqrt {2hy - {y^2}} }} \times \left( {2h - 2y} \right)$
$\therefore \dfrac{{dR}}{{dy}} = 0$
$ \Rightarrow \dfrac{2}{{\sqrt {2hy - {y^2}} }}\left( {2h - 2y} \right) = 0$
$ \Rightarrow 2h - 2y = 0$
By rearranging, we get
$y = h$
Therefore, the range of emerging stream will be maximum if $y = h.$
Therefore, from the above explanation correct option is (A) $h.$

Note:For maximum we need to have $\dfrac{{dR}}{{dy}} = 0$ and $\dfrac{{{d^2}R}}{{d{y^2}}} < 0$ is important.
But calculating $\dfrac{{{d^2}y}}{{d{y^2}}} < 0$ is important.
When we get more than one values of $y.$
But there in this equation we got only one value of $y,$ we can assume that it will be maximum at this point. Otherwise the question will not make any sense.