Question

A truck can move up a road having the grade of 1m rise for every 50m with a speed of 15km.hr. The resisting force is equal to 1/25^th the weight of the truck. How fast will the same truck move down the hill with the same horsepower?
1) 30km/hr
2) 45km/hr
3) 60km/hr
4) 75km/hr

Answer 1

Hint:Here, we have been given the angle in terms of rise and distance covered. Consider a truck moving in a triangular area. The perpendicular distance would be the rise and the hypotenuse would be the distance covered by the truck for every 1m rise. Find the net force in each condition.

Complete step by step solution:
The initial power of the truck is given by:
$P = \dfrac{W}{T}$ ;
Here:
P = Power;
W = Work;
T = Time;

Here, ${\text{Work = Force }} \times {\text{ Distance}}$;
 $P = \dfrac{{F \cdot D}}{T}$;
Now, we know that speed/velocity is distance/displacement upon time so:
\[ \Rightarrow P = F\dfrac{D}{T}\];
\[ \Rightarrow P = FV\];
For the initial case:
\[{P_1} = {F_1}{V_1}\];
For the final case:
\[{P_2} = {F_2}{V_2}\];
Step 2: Find out the angle:
We have been given the angle in terms of length covered and rise gained:

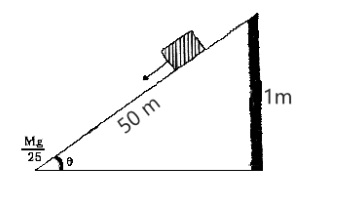
So, from the above diagram the sin angle will cover the perpendicular (rise) and the hypotenuse (length):
$\sin \theta = \dfrac{1}{{50}}$ ;
Now, the initial force when the truck is going upwards is:
${F_1} = mg\sin \theta + \dfrac{{mg}}{{25}}$ ;
Put the value of the angle in the above equation
$ \Rightarrow {F_1} = \dfrac{{mg}}{{50}} - \left( { - \dfrac{{mg}}{{25}}} \right)$;
$ \Rightarrow {F_1} = \dfrac{{3mg}}{{50}}$;
Similarly, force for the second case when the truck is coming downwards:
${F_2} = \dfrac{{mg}}{{25}} - mg\sin \theta $;
$ \Rightarrow {F_2} = \dfrac{{mg}}{{25}} - \dfrac{{mg}}{{50}}$;
$ \Rightarrow {F_2} = \dfrac{{mg}}{{50}}$;
Now, we have been given that the initial power of the truck is equal to the final power of the truck:
\[{P_1} = {F_1}{V_1} = {P_2} = {F_2}{V_2}\];
Put the given values in the above relation:
\[ \Rightarrow \dfrac{{3mg}}{{50}}{V_1} = \dfrac{{mg}}{{50}}{V_2}\];
\[ \Rightarrow \dfrac{3}{{50}}{V_1} = \dfrac{1}{{50}}{V_2}\];
Cancel out the commons:
\[ \Rightarrow 3{V_1} = {V_2}\];
Put the value of initial velocity:
\[ \Rightarrow {V_2} = 45km/hr\];

Option “2” is correct. The same truck will move down the hill with the velocity of 45 km/hr with the same horsepower.

Note:Here, we have been given only common factors between the two conditions that is power. Write the formula of power in terms of force and velocity and equate the two conditions with each other. Cancel out the common and get the velocity downhill.