Question

A triangular field has sides 120m, 80m, and 50m. Find its area. Also, find the cost of fencing it with barbed wire at Rs.20 per meter if a space of 3m wide is to be left for the entry gate on one of its sides. As vegetables are grown in the field for an orphanage, the fencing contractor reduced the rate of fencing by 25% (Use $\sqrt {15} = 3.88$ ).

Answer 1

Hint: In this question we have to find the area of the triangular field with the help of the length of sides given, for are we use Heron’s Formula to calculate the area, then we have to calculate the cost of fencing by remembering the cost is reduced by 25%. And the formula is given below.

Formula Used:
For finding the area of triangular field we use heron’s formula
Area =\[247 \times 15\] $\sqrt {s(s - a)(s - b)(s - c)} $
Where a, b, c are length of the sides of the triangle
 S is the semi perimeter of the triangle which is calculated by dividing the perimeter by 2
Perimeter of triangle will be = $a + b + c$
So, semi perimeter will by s=$\dfrac{{a + b + c}}{2}$
For reducing the cost by x percentage we use the below formula
${\text{Reduced cost = originalcost - originalcost} \times }\,{\text{ reduction}\% }$

Complete step by step answer:
The perimeter of the triangular field will be =$a + b + c$
Where a, b, c are the sides of the triangular field

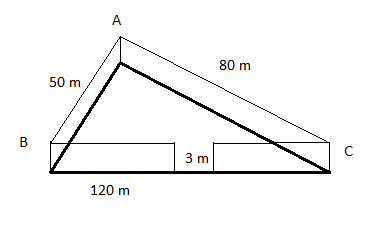
Here a =120m, b=80m, c=50m so putting the values in above formula we get,
Perimeter of triangular field
$120 + 80 + 50 = 250{\text{ cm}}$
Now we will calculate the value of semi perimeter by dividing above result by 2.
We get, Semi perimeter of triangular field = $\dfrac{{a + b + c}}{2}$
We get, = $\dfrac{{250}}{2}m$
Dividing 250 by 2 in above equation we get,
Semi perimeter= $125m$
Now, putting the values of semi perimeter and sides of triangular field we get,
Area= $\sqrt {s(s - a)(s - b)(s - c)} $
=$\sqrt {125(125 - 120)(125 - 80)(125 - 50)} $
Subtracting respective terms in above equation we get,
=$\sqrt {125(5)(45)(75)} $
Now, factorization above number so that they should be perfect square
$125 = 5 \times 5 \times 5$
$45 = 5 \times 9$
$75 = 5 \times 15$
Substituting above values we get,
=\[\sqrt {5 \times 5 \times 5(5)(5 \times 9)(5 \times 15)} \]
Making pair of 5 and taking square root of 9 we get,
=\[5 \times 5 \times 5 \times 3\sqrt {15} \]
Taking the value of $\sqrt {15} = 3.88$ as give in the question we get,
=\[375 \times 3.88\]
Multiplying above numbers we get the area,
=\[1455{m^2}\]
Hence the area of the triangular field will be \[1455{m^2}\]
Now we have to find the cost of fencing, for that first we will find the length of wire we needed for fencing,
Since According to question 3m should be left for gate
So we have to reduce 3m from the perimeter we calculated above
We get,
Length of wire needed for fencing=\[(250 - 3)m\]
That is, = \[247m\]
We have given the cost of one meter that is Rs 20 but due to vegetables grown in the field the rate is reduced
Now, we will calculate the reduced rate using formula stated above
${\text{Reduced cost = originalcost - originalcost} \times }\,{\text{ reduction}\% }$.
Here original cost is Rs20
And reduction % is given as 25%
Putting the values in the formula we get,
=\[20 - 20 \times \dfrac{{25}}{{100}}\]
Now multiplying 20 and 25 and then dividing by 100 we get,
=\[20 - \dfrac{{500}}{{100}}\]
=\[20 - 5\]
Now subtracting 5 from 20 we get the reduced rate for fencing the triangular field
=$Rs.15$ per meter
Now, we will calculate the cost of fencing by multiplying the length of wire needed and the new rate we calculated above
Cost of fencing = Rs.\[247 \times 15\]
Cost of fencing = Rs. $3705$

Hence the cost of fencing the triangular field is Rs 3705.

Note:
Use the proper formula for calculating the area of the triangle, analyze what is given in the question of what is asked, always factorization first to calculate the square root of the number to avoid mistakes while solving. As mention in the question, the use of Square root 15 should be is there in the answer, so be sure to use that in your answer as mention in the question given.