Question

A triangle is inscribed in a circle. The vertices of the triangle divide the circle into three arcs of length 3, 4 and 5 units then the area of the triangle is
(a) $\dfrac{9\sqrt{3}\left( 1+\sqrt{3} \right)}{{{\pi }^{2}}}$ sq. unit
(b) \[\dfrac{9\sqrt{3}\left( \sqrt{3}-1 \right)}{{{\pi }^{2}}}\] sq. unit
(c) \[\dfrac{9\sqrt{3}\left( 1+\sqrt{3} \right)}{2{{\pi }^{2}}}\] sq. unit
(d) \[\dfrac{9\sqrt{3}\left( \sqrt{3}-1 \right)}{2{{\pi }^{2}}}\] sq. unit

Answer 1

Hint: In this question, first create a figure to better understand the question and then using the circumference formula $C=2\pi R$, calculate the circumradius. Using the formula of arc length
\[S=R\theta \] find the value of the central angle. By using the Inscribed angle theorem which states that, the angle inscribed in the circle is equal to half of its central angle find the angles. Substitute these angles in the formula of circumradius $R=\dfrac{abc}{4\Delta }$ to find the area of triangle $\Delta $.

Complete step-by-step solution:
Let us create a figure of a triangle ABC inscribed inside the circle.

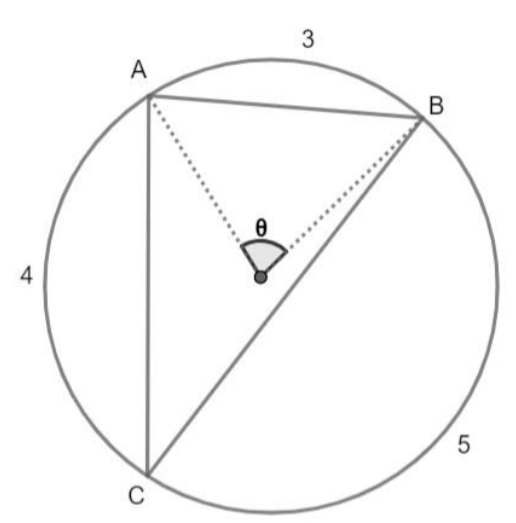
According to the figure we have, arc AB = 3, arc AC = 4, arc BC = 5
We know the circumference of a circle = $2\pi R$ and all the three arcs make a circle.
$C = 3 + 4 + 5$
$\begin{align}
  & 2\pi R=12 \\
 & R=\dfrac{12}{\begin{align}
  & 2\pi \\
 & =\dfrac{6}{\pi }
\end{align}}
\end{align}$
We know, arc length $S=R\theta $, $R=\dfrac{6}{\pi }$, $S=3$for arc AB
$\begin{align}
  & \theta =\dfrac{S}{R} \\
 & =\dfrac{3}{\dfrac{6}{\pi }} \\
 & =\dfrac{3\pi }{6} \\
 & =\dfrac{\pi }{2}
\end{align}$
Now, we know the circumradius of a triangle $R=\dfrac{abc}{4\Delta }$
Where, a, b and c denote the sides of the triangle and $\Delta $ is the area of the triangle, so the formula changes to $\Delta =\dfrac{abc}{4R}$……………………………..……..(i)
We know the sine rule or law,
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$
Therefore, we get
a = 2RsinA, b = 2RsinB, c = 2RsinC
Substitute the above a, b and c values in equation (i)
\[\Delta =\dfrac{\left( 2R\sin A \right)\left( 2R\sin B \right)\left( 2R\sin C \right)}{4R}\]
    $=2{{R}^{2}}\left( \sin A \right)\left( \sin B \right)\left( \sin C \right)$………………….. (ii)
Now, let us find the angles A, B and C.
With the help of inscribed angle theorem,
We know, \[\angle C=\dfrac{1}{2}\times \theta \]
$\begin{align}
  & \angle C=\dfrac{1}{2}\times \dfrac{\pi }{2} \\
 & =\dfrac{\pi }{4}
\end{align}$
Now, for angle A, we know $\theta =\dfrac{S}{R}$, $S=5$, $R=\dfrac{6}{\pi }$
We know, by Inscribed angle theorem, $\angle A=\dfrac{1}{2}\times \theta $
$\begin{align}
  & \angle A=\dfrac{1}{2}\times \dfrac{S}{R} \\
 & =\dfrac{1}{2}\times \dfrac{5}{\dfrac{6}{\pi }} \\
 & =\dfrac{5\pi }{2\times 6} \\
 & =\dfrac{5\pi }{12}
\end{align}$
We know that sum of all the angles of the triangle equal to 180 degree.
Therefore, $\angle A+\angle B+\angle C=180$
Substitute the values of A and C and find the value of B, note that $\pi =180{}^\circ $
We get,
$\begin{align}
  & \dfrac{5\pi }{12}+\angle B+\dfrac{\pi }{4}=180 \\
 & \angle B=180-75-45 \\
 & =60
\end{align}$
We have $\begin{align}
  & \angle A=\dfrac{5\pi }{12} \\
 & =75
\end{align}$
We can write $\sin \dfrac{5\pi }{12}=\sin 75$
So, $\sin (75) =\sin (30 + 45)$
Expand it by using the addition formulas in trigonometry transformation,
$\sin (X + Y) = \sin X \cos Y + \cos X \sin Y $
We get, $\sin (30 + 45) = \sin 30 \cos 45 + \cos 30 \sin 45$
                                     $\begin{align}
  & =\dfrac{1}{2}\times \dfrac{1}{\sqrt{2}}+\dfrac{\sqrt{3}}{2}\times \dfrac{1}{\sqrt{2}} \\
 & =\dfrac{1+\sqrt{3}}{2\sqrt{2}} \\
\end{align}$
Now, when you substitute all the values of angles A, B and C in the equation (ii) to find the area of triangle, we get
$\begin{align}
  & \Delta =2{{R}^{2}}\left( \dfrac{1+\sqrt{3}}{2\sqrt{2}} \right)\left( \dfrac{\sqrt{3}}{2} \right)\left( \dfrac{1}{\sqrt{2}} \right) \\
 & =2{{\left( \dfrac{6}{\pi } \right)}^{2}}\left( \dfrac{1+\sqrt{3}}{2\sqrt{2}} \right)\left( \dfrac{\sqrt{3}}{2\sqrt{2}} \right) \\
 & =2\left( \dfrac{36}{{{\pi }^{2}}} \right)\left( \dfrac{\sqrt{3}\left( 1+\sqrt{3} \right)}{4\cdot 2} \right) \\
 & =\dfrac{9}{{{\pi }^{2}}}\left( \dfrac{\sqrt{3}\left( 1+\sqrt{3} \right)}{1} \right) \\
 & =\dfrac{9\sqrt{3}\left( 1+\sqrt{3} \right)}{{{\pi }^{2}}}
\end{align}$
Hence, the area of the triangle is $\dfrac{9\sqrt{3}\left( 1+\sqrt{3} \right)}{{{\pi }^{2}}}$

Note: In this equation, make sure you solve the steps accordingly and be careful while solving a proof or which includes a tedious number of steps. There is another way to solve this same question, where the first few steps are similar and then you need to use the center of the circle and find the area of the triangle by finding the area of three different triangles which is divided into three parts of the original triangle with the help of central angle of each sub-divided triangle.