Question

A triangle has two corners with angles of $\dfrac{{2\pi }}{3}$ and $\dfrac{\pi }{6}$.If one side of the triangle has a length of $12$, what is the largest possible area of the triangle?

Answer 1

Hint: Here, in the given question, we are given that a triangle has two corners with angles of $\dfrac{{2\pi }}{3}$ and $\dfrac{\pi }{6}$. One side of the triangle has a length of $12$ and we need to find the largest possible area of the triangle. At first we will find the third angle of the triangle. Here, in the given question we will have a third angle equal to $\dfrac{\pi }{6}$. From here we can see that two angles are of the same measure, it means the given triangle is an isosceles triangle. So, we will have two different cases to find the area, one is when we have side $12$ opposite to $30^\circ $ angle and in other case we will find the area when side $12$ is opposite to $120^\circ $ angle. We will find the area in both the cases and compare them to which area is maximum.

Complete step by step answer:
We are given that the two angles of a triangle are $\dfrac{{2\pi }}{3}$ and $\dfrac{\pi }{6}$. As we know, the sum of angles of a triangle is $\pi $. So, from here we will find the third angle of the triangle. Let the third angle be $x$.
$x + \dfrac{{2\pi }}{3} + \dfrac{\pi }{6} = \pi $
$\Rightarrow x = \pi - \dfrac{{2\pi }}{3} - \dfrac{\pi }{6}$
On taking LCM, we get
$x = \dfrac{{6\pi - 4\pi - \pi }}{6}$
$\Rightarrow x = \dfrac{\pi }{6}$
Or we can write, $x = 30^\circ $.
From here we can conclude that we have an isosceles triangle because two angles are the same. It also means that we can get two different areas based on which side is $12$.

Case 1: If the side with a length of $12$ is opposite either $\dfrac{\pi }{6}$ or $30^\circ $ angle, then by the isosceles triangle theorem, the side opposite the other $30^\circ $ angle must also be $12$.

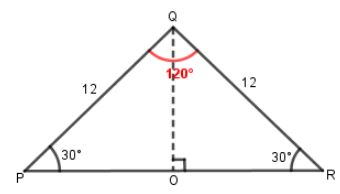
If we construct an altitude in the triangle as shown, we create two congruent triangles, with angles $\left( {30^\circ ,60^\circ ,90^\circ } \right)$. We know that side $PQ$ is double the length of side $QO$. Since $PQ$ is $12$, $QO$ is thus $6$. $\vartriangle PQO$ has angles of $30^\circ ,60^\circ ,90^\circ $. The shortest leg is across from the $30^\circ $ angle, the length of the hypotenuse is always double the length of the shortest leg, you can find the long leg by multiplying the short leg by the root of $3$. As we know the hypotenuse is the longest side in a right triangle, which is $12$. So, we have $QO = 6$ and $PR = 12\sqrt 3 $.With these measurements, we now have a base (side = $12\sqrt 3 $), and a height (side = $6$). We can use these values to find the triangle's area.
As we know, area of triangle = $\dfrac{1}{2} \times base \times height$. Therefore, we get
Area = $\dfrac{1}{2} \times 12\sqrt 3 \times 6$
Area = $36\sqrt 3 uni{t^2}$

Case 2: If the side opposite to the angle $120^\circ $ is $12$, we can apply the same logic as we did in case one. This time however, $PR$ is $12$.

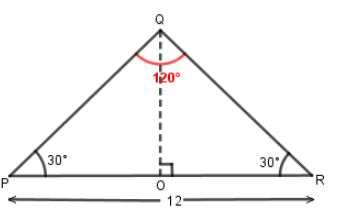
As we know altitude from the apex of an isosceles triangle bisects the base into two equal parts and also bisects its apex angle into two equal angles. Therefore, we have
$PO = OR = 6$
For altitude, we have
$ \Rightarrow QO \times \sqrt 3 = PO$
$ \Rightarrow QO = \dfrac{6}{{\sqrt 3 }}$
Now, we have base = $12$, height = $\dfrac{6}{{\sqrt 3 }}$. Therefore, we get
Area = $\dfrac{1}{2} \times 12 \times \dfrac{6}{{\sqrt 3 }}$
Area = $\dfrac{{36}}{{\sqrt 3 }}uni{t^2}$
As we know $36\sqrt 3 > \dfrac{{36}}{{\sqrt 3 }}$.

Therefore, the largest possible area is $36\sqrt 3 \,uni{t^2}$.

Note: To solve this type of question, first we need to understand which type of triangle is given in the question. After this using properties of the triangle find the area of the triangle using formulae. We should be careful about the unit. Calculation should be done in the same unit. We should take care of the calculations so as to be sure of our final answer.There are other formulas too to find the area of the triangle. For example:
Area of a right-angled triangle = $\dfrac{1}{2} \times base \times height$
Area of an equilateral triangle = \[\dfrac{{\sqrt 3 }}{4} \times sid{e^2}\]
Area of an isosceles triangle = $\dfrac{1}{4} \times b \times \sqrt {4{a^2} - {b^2}} $ ($b$ is the base and $a$ is the measure of one of the equal sides.