Question

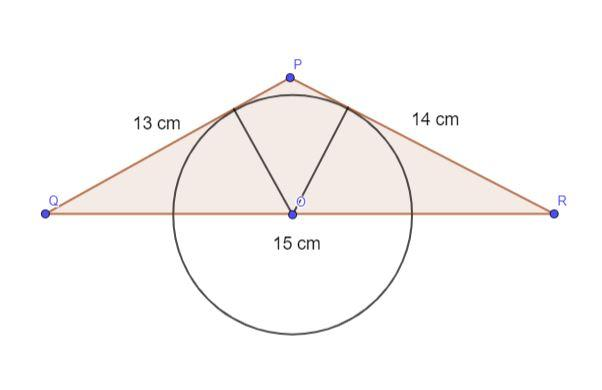
A triangle has sides with lengths 13 cm, 14 cm and 15 cm. A circle whose centre lies on the longest side touches the other two sides. The radius of the circle is (in cm)$\underline{\,\,\,\,\,\,\,\,\,\,\,\,\,}$.

Answer 1

Hint: The radius of the circle is equal to the height of either of the small triangles (from figure). Divide the bigger triangle into two ($\Delta POQ$and $\Delta POR$ ). Equate the area of the bigger triangle to the sum of the smaller triangles. Use Heron’s formula to find the area of the given triangle. According to Heron’s formula, if a, b and c are the sides of a triangle and ‘s’ is the semi-perimeter of the triangle, then,
$s=\dfrac{a+b+c}{2}$
Area of the triangle$=\sqrt{s(s-a)(s-b)(s-c)}$

Complete step by step answer:
We are given a triangle that has sides with length 13 cm, 14 cm and 15cm. Let PQ= $a$ (=13 cm), PR= \[b\] (=14 cm) and QR= $c$ (=15 cm)
We have to find the radius of the circle whose centre lies on the longest side and touches the other two sides. Let $r$ be the radius of the circle.
Join the point P to the centre of the circle O.

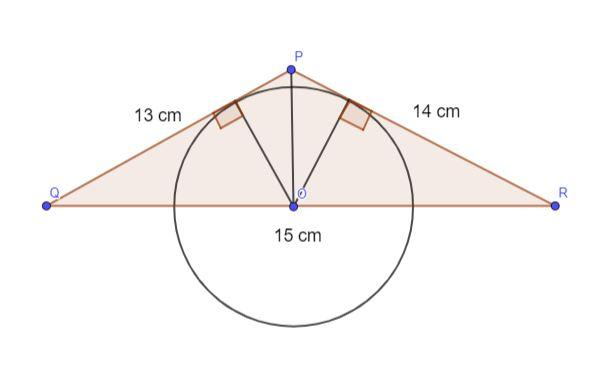
From the figure it is clear that the perpendicular drawn from the centre of the circle to the two smaller sides of the triangle are the heights of the smaller triangles ($\Delta POQ\,and\,\Delta POR$ ).
We an find the semi-perimeter of the triangle PQR using $s=\dfrac{a+b+c}{2}$
So, substituting values, we get
$\Rightarrow s=\dfrac{13+14+15}{2}$
$\Rightarrow s=\dfrac{13+14+15}{2}=\dfrac{42}{2}=21\,cm$

Using Heron’s formula, we have
Area of the triangle PQR$=\sqrt{s(s-a)(s-b)(s-c)}$
Again, substituting values, we get
$\Rightarrow A=\sqrt{21(21-13)(21-14)(21-15)}$
$\Rightarrow A=\sqrt{21\times (8)\times (7)\times (6)}$
$\Rightarrow A=\sqrt{3\times 7\times 2\times 2\times 2\times 7\times 2\times 3}$
$\Rightarrow A=3\times 7\times 2\times 2$
$\Rightarrow A=84\,c{{m}^{2}}$
$\therefore $ Area of the triangle PQR$=84\,c{{m}^{2}}$
From figure we have,
Area of the triangle PQR = Area of $\Delta POQ$+ Area of $\Delta POR......................(1)$
We know that,
Area of a triangle \[=\dfrac{1}{2}\times \] Base$\times $ Height
For $\Delta POQ$,
Base = PQ, Height = radius of the circle = $r$
Therefore, we get Area of $\Delta POQ$\[=\dfrac{1}{2}\times \] PQ$\times $$r$
\[=\dfrac{1}{2}\times 13\times r\]
$\therefore $ Area of $\Delta POQ$ $=\dfrac{13r}{2}\,c{{m}^{2}}\,...................(2)$
For $\Delta POR$,
Base = PR, Height = radius of the circle = $r$
Therefore, we get Area of $\Delta POR$\[=\dfrac{1}{2}\times \] PR$\times $$r$
\[=\dfrac{1}{2}\times 14\times r\]
$\therefore $ Area of $\Delta POR$$=\dfrac{14r}{2}=7r\,c{{m}^{2}}\,...................(3)$
Substituting (2) and (3) in equation (1), we get,
Area of the triangle PQR = Area of $\Delta POQ$+ Area of $\Delta POR$
$=\dfrac{13r}{2}+7r$
But, area of the triangle PQR$=84\,c{{m}^{2}}$
$\therefore 84=\dfrac{13r}{2}+7r$
On taking LCM, we will get
$\therefore 84=\dfrac{13r}{2}+\dfrac{14r}{2}$
$\Rightarrow 168=27r$
$\therefore r=\dfrac{168}{27}\,cm\,=\,6.22\,cm$

Hence, the radius of the circle is 6.22 cm.

Note: Keep every measurement in the same unit. If the units differ, make necessary conversions. While finding the area of the triangle using Heron’s formula, rather than directly taking the root using the long division method, look for chances of simplification. The semi-perimeter of the triangle is simply half the perimeter of the triangle. The sides PQ and PR of the triangle PQR are tangents of the circle with centre at O.
According to the property of circles, the line joining the point of contact of the tangent and the centre is perpendicular to the tangent. Hence, we take this perpendicular as the smaller triangles’ heights (altitudes).