Question

A triangle has sides 6,7, and 8. The line through its incenter parallel to the shortest side is drawn to meet the other two sides at P and Q. Then find the 7 times the length of the segment PQ.

Answer 1

Hint: Firstly we should know that we can calculate the area of the triangle with the help of the radius and with the help of height and base. In this question we have to use the formula of $ \Delta = r \times s $ and $ \Delta = \dfrac{1}{2} \times b \times h $ , then compare and proceed accordingly.

Complete step-by-step answer:
Given, a triangle has sides 6, 7 and 8 respectively.
Then, the perimeter will be $ 6 + 7 + 8 = 21 $ .
A line is passing through the incenter.
We need to find the length of that line passing through the incenter first.
Consider a triangle ABC and let D be the incenter of the triangle, as shown in the figure.

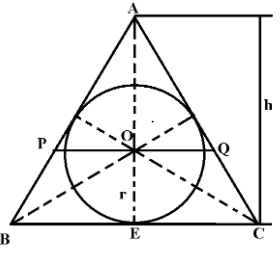
We are considering BC as the smallest side, whose size is 6.
Let r be radius of the circle then the area of the triangle will be given by,
 $ \Delta = r \times s $ , where s is the semi-perimeter.
So, $ s = \dfrac{{21}}{2} $ .
Therefore,
 $
\Rightarrow \Delta = r \times s \\
\Rightarrow \Delta = r \times \dfrac{{21}}{2} \\
  $ ………….(i)
Area of triangle can also be calculated as,
 $ \Delta = \dfrac{1}{2} \times b \times h $ ……….(ii), here base is 6 and height is h.
Now, compare equation (i) and (ii).
 $
\Rightarrow r \times \dfrac{{21}}{2} = \dfrac{1}{2} \times b \times h \\
\Rightarrow r \times 21 = 6 \times h \\
\Rightarrow \dfrac{r}{h} = \dfrac{6}{{21}} \\
\Rightarrow \dfrac{r}{h} = \dfrac{2}{7} \\
  $
Now consider triangle ABC and triangle APQ, as both are similar triangles.
So, $ \dfrac{{AO}}{{AE}} = \dfrac{{PQ}}{{BC}} $
 $
\Rightarrow \dfrac{{h - r}}{h} = \dfrac{{PQ}}{6} \\
\Rightarrow 1 - \dfrac{r}{h} = \dfrac{{PQ}}{6} \\
\Rightarrow 1 - \dfrac{2}{7} = \dfrac{{PQ}}{6} \\
\Rightarrow \dfrac{{7 - 2}}{7} = \dfrac{{PQ}}{6} \\
\Rightarrow \dfrac{5}{7} = \dfrac{{PQ}}{6} \\
\Rightarrow PQ = \dfrac{{30}}{7} \\
  $
In the question we need to find seven times PQ, so $ 7 \times PQ = 7 \times \dfrac{{30}}{7} = 30 $ .

Note: Incenter of a triangle is the point inside any circle where all the angle bisectors of a triangle intersect. Perimeter is the length of the outline of any 2-D figure and perimeter of any triangle is the sum of the sides and semi-perimeter is the half of the perimeter. It is generally denoted by “s”.