Question

A triangle cannot have more than ___ right angle(s).
A) one
B) two
C) three
D) zero

Answer 1

Hint: The question requires us to find out the answer using the properties of triangles. Right-angled triangle is such a triangle where one angle is right-angled. If there will be more than one right-angle, the shape will not remain a triangle.

Complete step by step solution:
Triangle with one \[{90^ \circ }\] angle is known as right-angled triangles. Since one of the angles is \[{90^ \circ }\], the sum of the other two angles is also \[{90^ \circ }\].
A triangle has three sides: base, perpendicular and hypotenuse.
Consider the following diagram:

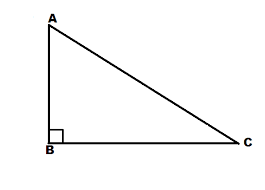
Here, \[m\angle B = {90^ \circ }\]and \[\vartriangle ABC\]is a right-angled triangle.
The sum of all the angles of a triangle is \[{180^ \circ }\].
So, we can say that \[\angle A + \angle B + \angle C = {180^ \circ }\]
\[\angle A + 90 + \angle C = {180^ \circ }\]
\[\angle A + \angle C = {180^ \circ } - {90^ \circ }\]
\[\angle A + \angle C = {90^ \circ }\]
Hence the sum of both the angles will be \[{90^ \circ }\]and none of them can be zero i.e.
\[m\angle A \ne 0\]
\[m\angle C \ne 0\]
Hence, we can conclude that:
There can never be two or more right angles in a triangle. A triangle has three sides, and the interior angles add up to 180 degrees. If a triangle has two right angles, the third angle must be 0 degrees, implying that the third side would overlap the other. As a result, a triangle with two right angles is not feasible.
Thus, a triangle cannot have more than one right angle. So, option (A) is correct.

Note:
Trigonometric functions or the Pythagoras theorem can be used to find the missing sides of a right-angled triangle. The Pythagoras theorem can be used if two sides are given, and trigonometric functions like sine, cos, and tan can be used to find the missing side if one side and an angle are given.