Question

A triangle ABC with vertices A (-1, 0), B (-2, 3/4) and C (-3, -7/6) has its orthocenter H, then the orthocenter of the triangle BCH will be:
$\left( a \right)$ (-3, -2)
$\left( b \right)$ (1, 3)
$\left( c \right)$ (-1, 2)
$\left( d \right)$ None of these

Answer 1

Hint – In this question first draw perpendicular from vertices A, B and C (see figure) onto the sides BC, AC and AB respectively, then find the orthocenter of triangle ABC i.e. the coordinates of H, then form a triangle HBC and again draw perpendicular from vertices H, B and C onto the sides BC, HC and HB, this will help getting the orthocenter of the triangle HBC.

Complete step by step solution:

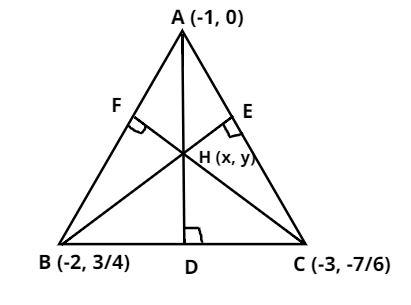
Consider the triangle ABC having vertices (-1, 0), (-2, 3/4) and (-3, -7/6).
Draw the perpendicular from the vertices on the line BC, AC and AB which cuts the line BC, AC and AB at the points D, E and F respectively
So the altitudes of triangles are AD, BE and CF as shown in figure, where altitudes are nothing but the perpendicular line.
So the orthocenter of the triangle is the intersection point of the altitudes.
Let orthocenter be H = (x, y).
So find out any two equations of the altitude and solve them which is the required orthocenter of the triangle.
Now to calculate the slope of the sides of the triangle. The formula to calculate the slope is given as,
Slope of a line = $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
To calculate the perpendicular slope of the sides of the triangle. It gives us the slope of the altitudes of the triangle. The formula to calculate the perpendicular slope is given as,
Perpendicular slope of a line = $\dfrac{{ - 1}}{{{\text{slope of a line}}}}$
To calculate the equation for the altitudes with their respective coordinates. The point-slope formula is given as,
$y - {y_1} = m\left( {x - {x_1}} \right)$, Where m is the slope of the altitude.
Let A = $\left( {{x_1},{y_1}} \right)$ = (-1, 0)
B = $\left( {{x_2},{y_2}} \right)$ = (-2, 3/4)
C = $\left( {{x_3},{y_3}} \right)$ = (-3, -7/6)
Therefore slope of line AB = $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$= $\dfrac{{\dfrac{3}{4} - 0}}{{ - 2 - \left( { - 1} \right)}} = \dfrac{{\dfrac{3}{4}}}{{ - 1}} = \dfrac{{ - 3}}{4}$
Therefore slope of altitude CF, (m) = $\dfrac{{ - 1}}{{{\text{slope of line AB}}}} = \dfrac{{ - 1}}{{\dfrac{{ - 3}}{4}}} = \dfrac{4}{3}$
Therefore equation of line CF is
$y - {y_3} = m\left( {x - {x_3}} \right)$
Now the line is passing through point C = $\left( {{x_3},{y_3}} \right)$ = (-3, -7/6)
$ \Rightarrow y - \dfrac{{ - 7}}{6} = \dfrac{4}{3}\left( {x - \left( { - 3} \right)} \right)$
$ \Rightarrow y + \dfrac{7}{6} = \dfrac{4}{3}\left( {x + 3} \right)$
$ \Rightarrow \dfrac{{6y + 7}}{6} = \dfrac{{4x + 12}}{3}$
$ \Rightarrow 6y + 7 = 8x + 24$
$ \Rightarrow 6y - 8x = 24 - 7 = 17$.................. (1)
Now slope of line BC = $\dfrac{{{y_3} - {y_2}}}{{{x_3} - {x_2}}}$= $\dfrac{{\dfrac{{ - 7}}{6} - \dfrac{3}{4}}}{{ - 3 - \left( { - 2} \right)}} = \dfrac{{\dfrac{{ - 14 - 9}}{{12}}}}{{ - 1}} = \dfrac{{ - 23}}{{ - 12}} = \dfrac{{23}}{{12}}$
Therefore slope of altitude AD, (m1) = $\dfrac{{ - 1}}{{{\text{slope of line BC}}}} = \dfrac{{ - 1}}{{\dfrac{{23}}{{12}}}} = \dfrac{{ - 12}}{{23}}$
Therefore equation of line AD is
$y - {y_1} = {m_1}\left( {x - {x_1}} \right)$
Now the line is passing through point A = $\left( {{x_1},{y_1}} \right)$ = (-1, 0)
$ \Rightarrow y - 0 = \dfrac{{ - 12}}{{23}}\left( {x - \left( { - 1} \right)} \right)$
$ \Rightarrow 23y = - 12\left( {x + 1} \right)$
$ \Rightarrow 12x + 23y = - 12$..................... (2)
Now from equation (1)
$ \Rightarrow x = \dfrac{{6y - 17}}{8}$................... (3)
Now substitute this value in equation (2) we have,
$ \Rightarrow 12\left( {\dfrac{{6y - 17}}{8}} \right) + 23y = - 12$
Now simplify this equation we have,
$ \Rightarrow 3\left( {\dfrac{{6y - 17}}{2}} \right) + 23y = - 12$
$ \Rightarrow 18y - 51 + 46y = - 24$
$ \Rightarrow 64y = 51 - 24 = 27$
$ \Rightarrow y = \dfrac{{27}}{{64}}$
Now substitute this value in equation (3) we have,
$ \Rightarrow x = \dfrac{{6 \times \dfrac{{27}}{{64}} - 17}}{8} = \dfrac{{ - 463}}{{256}}$
So the orthocenter of the triangle ABC is
H = (x, y) = $\left( {\dfrac{{ - 463}}{{256}},\dfrac{{27}}{{64}}} \right) = \left( {1.808,0.422} \right)$
Now we have to find the orthocenter of triangle BCH.
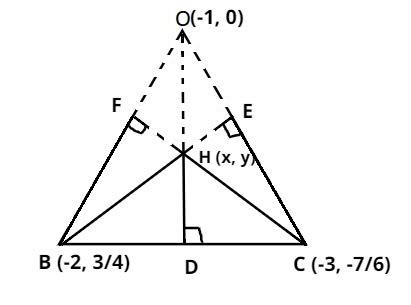
Now let the orthocenter of triangle BCH is O which is the intersection of the altitudes from the vertices of the triangle on the opposite sides of the triangle BCH.
As it is not possible to draw the altitudes on sides BH and CH internally so these altitudes are outside the triangle BCH as shown in figure 2, it meets a point O which is the required orthocenter of the triangle BCH as shown in the second figure.
Now as we see that the point O and the point A are the same, so the orthocenter of the triangle BCH is nothing but the coordinates of A.
So the orthocenter of the triangle BCH is = coordinates of A = (-1, 0)
So this is the required answer.
Hence option (D) none of these is the correct answer.

Note – The trick point here was that why have we drawn perpendiculars from different vertices. The reason behind this was by definition of orthocenter it is simply the intersection of the altitudes of the triangle, so we intended to find the equation of altitudes of triangles so that the point of intersection of them can be taken out. The concept of line that if two lines are perpendicular then their slopes are related as ${m_1} \times {m_2} = - 1$, helps finding the point of intersection that is the orthocenter.