Question

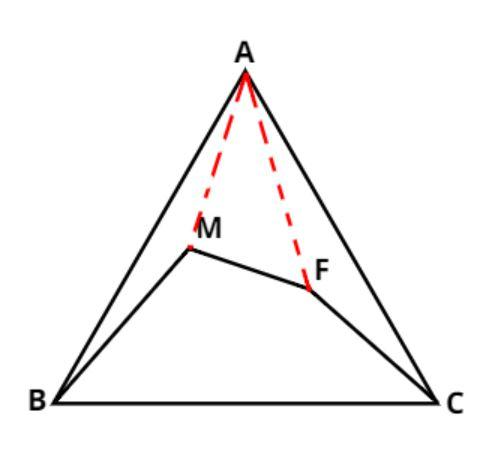
A triangle ABC with points F and M lying inside the triangle such that BCFM is a convex quadrilateral. Now show that the perimeter of ABC is greater than the perimeter of BCFM.

Answer 1

Hint – In this particular question first draw the pictorial representation of the problem which will give us a clear picture of what is asked, then join the points AM and AF respectively so use these concepts to reach the solution of the question.

Complete step-by-step answer:

Proof –
Consider the triangle ABC as shown above.
Now the points F and M are the points which are inside the triangle as shown in the above figure.
Now join CF, FM and MB as above to make a convex quadrilateral (i.e. the angle of the interior angles of the convex quadrilateral is less than 180 degree).
Now join the points MA and FA.
So that it makes three more triangles which are AMB, AFC and AMF
Now as we know that in a triangle the sum of any two sides is always greater than the third side otherwise the triangle is not possible.
So in triangle AMB we have,
AM + MB > AB............... (1)
Now in triangle AFC we have,
AF + FC > AC................... (2)
And in triangle AMF we have,
AM+AF > FM
It is written as
AM + AF = FM + q................. (3), where q>0
Now add equation (1) and (2) we have,
AM + MB + AF + FC > AB + AC
Now add both sides by BC we have,
FM + MB + FC + BC > AB + AC + BC
Now from equation (3) we have,
FM + q + MB + FC + BC > AB + AC + BC
Now rearranging the terms we have,
BC + CF + FM + MB + q > AB + BC + CA............... (4)
Now as we know that the perimeter of any shape is the sum of all the side lengths.
So the perimeter of the triangle is ${P_\Delta }$ = AB + BC + CA
And the perimeter of the convex quadrilateral is ${P_{qua}}$= BC + CF + FM + MB
Now substitute these values in the equation (4) we have,
$ \Rightarrow {P_{qua}}$ + q >${P_\Delta }$................... (5)
So as we see that the perimeter of quadrilateral plus q (which is greater than zero) is greater than the perimeter of the triangle.
Now as we see that in the triangle AFM, AM + AF = FM + q, here q is some positive quantity but as we see from the figure the value of the q should be large to satisfy this equation.
So from equation (5) we can say simply that if q is not present then the perimeter of the triangle is greater than the perimeter of the quadrilateral.
Therefore, ${P_\Delta }$(ABC) > ${P_{qua}}$ (BCFM)
Hence proved.
Note – Whenever we face such types of questions the key concept we have to remember is that in any triangle the sum of two sides is always greater than the third side so consider all the triangles in the diagram as above and make the equations according to above written property then add first two equations and use the third equation in the resultant equation after that add both sides BC and simplify as above we will get the required result.