Question

A triangle, a parallelogram, and a rectangle have the same base and are situated between the same parallels. The ratio of their areas is?

Answer 1

Hint: We are given that a triangle, a rectangle and a parallelogram have a common base and lie between common parallels. First of all, to understand the question better, draw the figure neatly. After that we will be using the formulas for area of triangle and area of parallelogram to find our ratio.
 $ \to $ Area of triangle $ = \dfrac{1}{2} \times base \times height $
 $ \to $ Area of parallelogram $ = base \times height $

Complete step-by-step answer:
In this question, we are given that a triangle, a parallelogram and a rectangle have the same base and are situated between the same parallels and we have to find the ratio of the areas of triangle and parallelogram.
Now, let us draw the figure for this condition first.

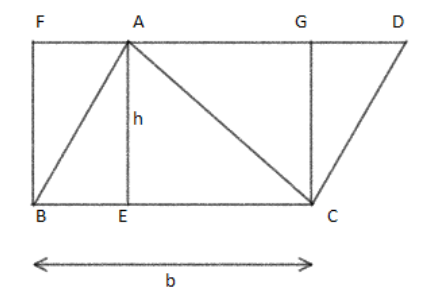
In the above figure, we can see that two lines AD and BC are parallel to each other.
The above figure contains three shapes: a rectangle, a triangle and a parallelogram.
There is $ \Delta ABC $ , $ \square FCGB $ and .
Now, all these three shapes have a common base BC and we have taken the base as b.
 $ BC = b $
Now, AE is the height of the parallelogram and triangle and we have taken the height as h.
 $ AE = h $
Now, we have to find the ratio of area of triangle to area of parallelogram.
Let us see the formulas for the areas of triangle and parallelogram.
 $ \to $ Area of triangle $ = \dfrac{1}{2} \times base \times height $
 $ \to $ Area of parallelogram $ = base \times height $
So, in our figure, base is b and height is h. Therefore,
 $ \to $ Area of $ \Delta ABC = \dfrac{1}{2}bh $
 $ \to $ Area of parallelogram = bh
Therefore, their ratio will be
 $ \to $ Ratio of area of $ \Delta ABC $ to parallelogram
 $ = \dfrac{{\dfrac{1}{2}bh}}{{bh}} $
Here, $ bh $ gets cancelled. Therefore,
 $ \to $ Ratio of area of $ \Delta ABC $ to
Hence, the ratio of the areas of $ \Delta ABC $ to is $ \dfrac{1}{2} $ .
So, the correct answer is “ $ \dfrac{1}{2} $ ”.

Note: Other important theorems are that
Parallelograms lying under the same parallels have equal areas.
Triangles lying the same parallel have equal areas.
Rectangles lying under the same parallels have equal areas.